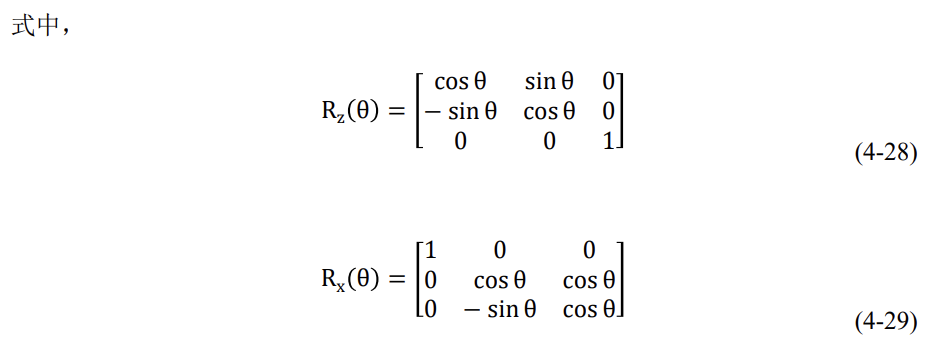GPS卫星位置解算

创始人

2024-05-27 11:43:38

0次

本文介绍了基于C语言的GPS卫星位置解算原理与程序设计。针对每个原理、公式、代码设计进行了详细讲解，希望能够给测绘学子们带来帮助。

参考书籍：

李征航黄劲松：GPS测量与数据处理（第三版）

基础原理

1）卫星位置解算流程

2）卫星有关参数

3）卫星位置计算过程

程序设计

数据预处理

1）GPS时转换(TimetoGPSsec)

2）选择最佳历元(select_epoch)

代码与解析

BDS卫星位置

基础原理

1）卫星位置解算流程

如流程图所示，在程序设计中对于一颗卫星的位置解算，是要经过多次迭代，直到信号传播时间收敛。

2）卫星有关参数

在正式开始程序设计之前，我们还需要了解一下卫星的相关参数及其含义。

平近点角M

卫星平均运动角速度为 $n=\frac{2\Pi \ }{T}\$ ，根据开普勒第三定律得：

$\frac{T^{2}}{a^{3}}=\frac{4\Pi ^{2}}{GM}$

所以卫星平均运动角速度n：

$n= \sqrt{\frac{GM}{a^{3}}}$

因此，平近点角M定义为：

$M= n\left ( t-t_{0} \right )$

t为信号发射时刻，t0为卫星过近地点时刻。

偏近点角E

如下图所示：以卫星椭圆轨道的焦点为原点，以指向近地点的方向为X轴，Y轴平行于椭圆短半轴，建立轨道平面坐标系。以卫星椭圆中心为圆心，以卫星轨道的长半轴a为半径作一个辅助圆。

过卫星S作X轴的垂线，其延长线与辅助圆交于S‘，圆心到S’的向径与X轴的夹角定义为偏近点角E。

平近点角与偏近点角的关系可用开普勒方程表示：

$M= E-e\sin E$

在计算偏近点角E时，E0可用平近点角M做初始值，然后进行迭代计算，因为E非常小，因此迭代几次即可收敛，可将收敛标准设为1.0e-5。

真近点角V

由上图所示，真近点角V与偏近点角E存在着一定关系，真近点角V可又下述式子得出：

$V=\arctan \frac{\sqrt{1-e^{2}}\sin E}{\cos E-e}$

其中，e为第一偏心率。

如果已知真近点角，那么卫星在轨道坐标系中的位置向量可以表示为：

$r= \frac{a\left ( 1-e^{2} \right )}{1+e\cos V}\binom{cosV}{sinV}$

卫星的运动速度

由上式得得卫星的运动速度为：

$r= \frac{na}{1-e\cos E}\binom{-sinE}{\sqrt{1-e^{2}\cos E}}$

由开普勒方程可得：

$\widehat{M}=\widehat{E}\left ( 1-e\sin E \right )= n$

因此，可以推导出卫星的运动方程：

$\widehat{r}=\frac{GM}{r^{3}}r$

卫星钟差

卫星钟差方程为：

$\Delta t_{s}=a_{0}+a_{1}(t-t_{oc})+a_{2}(t-t_{oc})^{2}+\Delta t_{r}$

a0，a1，a2为N文件中的钟频，钟偏和钟漂。（广播星历中的卫星钟差误差为10ns，等效距离为3m）

$\Delta t_{r}=-\frac{2\sqrt{A\cdot GM}}{c^{2}}e^{2}sinE$

其中 $\sqrt{A}$ 为长半轴a的平方根，e为轨道偏心率，二者都由广播星历播发；GM为引力常数，大小为：398600500000000；E为卫星的偏近点角。(因为偏近点角E很小，该误差在伪距中可忽略不计)

3）卫星位置计算过程

（1）求平均角速度n：

$n_{0}=\sqrt{\frac{GM}{a^{3}}}$

$n=n_{0}+\Delta n$

$\Delta n$ 为广播星历(N文件)中卫星平均运动速率与计算值之差（ $\Delta n$ 代码中用deltan表示）。

（2）求规划时刻 $t_{k}$

$t_{k}=t-t_{oe}$

t为信号发射时刻， $t_{oe}$ 为N文件中的参考历元（ $t_{oe}$ 代码中用TOE表示）。

信号发射时刻为：O文件观测时刻-信号传播时间。

近似信号传播时间=伪距观测值/光速-接收机钟差+卫星钟差+电离层改正+对流层改正

上式中，用参考时刻toe时刻代替了卫星过近地点t0时刻。

这是因为：广播星历2h更新一次，间给参考时刻设在中央时刻时，外推间隔小于1h。而卫星的运行周期为12h，采取卫星过近地点时刻t0，外推间隔最大可能达到6h。用toe代替t0，模型简单，并且可以保证精度。

计算t和toe时，需要保证二者之差在两小时内，计算才能生效。因此，在计算卫星位置前，需要根据O文件中的观测选择N文件中的最佳观测历元（代码见后文）。

（3）求平近角 $M$

$M=M_{0}+nt_{k}$

$M_{0}$ 为N文件中的参考时间的平近点角。

（4）求偏近点角E

$E_{0}=M$

$E_{n}=M+e\sin E_{n-1}$

e为N文件中轨道偏心率；偏近点角需要迭代计算，将平近角M作为E的初始值带入，因为E很小，一般迭代几次即可收敛，收敛条件为

$\left | E_{n}-E_{n-1} \right |< 1e-12$

1.0e-12为科学计数法，表示10的负12次方。

（5）求真近点角 $V$

$V=\arctan \frac{\sqrt{1-e^{2}}\sin E_{n}}{\cos E_{n}-e}$

（6）求升交角距u

$U=V_{k}+\omega$

$\omega$ 为N文件中的近地点角距（ $\omega$ 代码中用omega表示）。

（7）摄动改正

升交角距改正项： $\delta _{u}=C_{uC}\cos 2U+C_{uS}\sin 2U$

轨道向径改正项： $\delta _{r}=C_{rC}\cos 2U+C_{rS}\sin 2U$

轨道向径改正项： $\delta _{i}=C_{iC}\cos 2U+C_{iS}\sin 2U$

$C_{uC}C_{uS}C_{rC}C_{rS}C_{iC}C_{iS}$ 分别为N文件中提供的6个摄动改正参数。（ $\delta _{u}\delta _{r}\delta _{i}$ 在代码中分别用Epsilon_u、Epsilon_r、Epsilon_i表示）

（8）计算改正后的升交角距、轨道向径、轨道向径

$u_{k}=t_{k}+\delta _{u}$

$r_{k}=a\left ( 1-e\cos E_{k} \right )\delta _{r}$

$i_{k}=i_{0}+t_{k}\left ( IDOT \right )+\delta _{i}$

（9）卫星在升交点轨道直角坐标系的坐标

$x_{k}=r_{k}\cos u_{k}$

$y_{k}=r_{k}\sin u_{k}$

（10）计算升交点经度L

$L=\Omega _{0}+\left ( \Omega -\omega _{e} \right )t_{k}-\omega_{e} t_{oe}$

$\Omega _{0}$ 为N文件中GPS周开始时刻的升交点经度， $\Omega$ 为N文件中升交点赤经变化率， $t_{oe}$ 为N文件中参考历元时刻。

（11）计算卫星在地固坐标系中的空间直角坐标系

$X=x_{k}\cos L-y_{k}\cos i_{k}sinL$

$Y=x_{k}\sin L-y_{k}\cos i_{k}cosL$

$Z_{k}=y_{k}sini_{k}$

（12）计算Z轴旋转变换，得到的新坐标

$x=\cos \left ( e_{E}\Delta t \right )X+\sin \left ( e_{E} \Delta t\right )Y$

$y=-\sin\left ( e_{E}\Delta t \right )X+\cos \left ( e_{E} \Delta t\right )Y$

$z=Z$

$e_{E}$ 为地球自转角速度， $\Delta t$ 为信号传播时间。

（13）重新计算卫地距

$R=\sqrt{\left ( x-x_{r} \right )^{2}+\left ( y-y_{r} \right )^{2}+\left ( z-z_{r} \right )^{2}}$

$x_{r}y_{r}z_{r}$ 为接收机坐标，可将O文件中接收机概略坐标当作接收机坐标初始值，减少迭代次数。

（14）重新计算信号传播时间

$t=\frac{R}{Cv}$

R为新的卫地距，Cv表示光速。

（15）重复步骤1~14，直到信号传播时间收敛，收敛条件为

$\left | t_{n}-t_{n-1} \right |<0.0001$

程序设计

单颗卫星位置解算流程：

将年月日转换成GPS周内秒
为卫星选择最佳历元
计算信号近似传播时间
卫星位置解算

数据预处理

1）GPS时转换(TimetoGPSsec)

GPS时，也称GPS time，GPST，由GPS星载原子钟和地面监控站原子钟组成的一种原子时基准，其起点为1980年1月6日0时00分00秒。

观测值文件中的参考时刻是以年月日进行记录的，不利于计算，需转换成周内秒的形式。

程序设计主要思想：

先计算到1980年1月1号0时有多少天
考虑闰年（4年一润，百年不润，四百年一润），闰月（润年润月为29天），以及大小月。
1980年1月6日为星期日，一周的开始，解算出来的天数需要减6（1980.1.6为GPS时起算时刻）
将得到天数除以7，得到周内的天数，将周内天数转换成周内秒数

TimetoGPSsec代码如下：

double TimetoGPSsec(int year, int month, int day, int hour, int min, double sec)
{int DayofYear = 0, DayofMonth = 0, SecofWeek = 0;int i = 0;for (i = 1980; i < year; i++){//判断闰年if ((i % 4 == 0 && i % 100 != 0) || i % 400 == 0)DayofYear += 366;elseDayofYear += 365;}for (i = 1; i < month; i++){//判断大小月if (i == 1 || i == 3 || i == 5 || i == 7 || i == 8 || i == 10 || i == 12)DayofMonth += 31;else if (i == 4 || i == 6 || i == 9 || i == 11)DayofMonth += 30;else{if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0)DayofMonth += 29;elseDayofMonth += 28;}}int Day = DayofYear + DayofMonth + day - 6;//计算到1980年1月6号（星期日）有多少天SecofWeek = (double)(Day % 7) * 24 * 60 * 60 + (double)hour * 3600 + (double)min * 60 + sec;return SecofWeek;
}

其中：

传入的参数为O、N文件中得到的年、月、日、时、分、秒。
返回值为计算得到的周内秒。

2）选择最佳历元(select_epoch)

根据卫星的PRN号以及观测时间，选择与N文件中时间间隔最小的数据块进行解算。

主要思想：

遍历整个N文件数据块部分
先判断卫星的PRN号是否相等
设置最小时间差初始值为10000秒，每次更新最小值，并记录最小值所对应的历元数
返回时间差最小的历元数

select_epoch代码如下：

//挑选合适的星历
extern int select_epoch(double SecofWeek, int sPRN, pnav_body nav_b, int n_n)
{int n_epoch = 0;double min=10000;//假设最小值是1万秒double Min;int i;for (i = 0; i < n_n / 8; i++){if (sPRN == nav_b[i].sPRN){Min = fabs(SecofWeek - nav_b[i].TOE);if (Min <= min){n_epoch = i;min = Min;}}}return n_epoch;
}

其中：

SecofWeek为观测时刻的GPS周内秒，sPRN为卫星的PRN号，nav_b为导航文件数据块结构体，n_n为导航文件数据块总行数（不包含头部）
需要传入的参数有：观测的周内秒时间、卫星的PRN号、N文件中数据块的结构体以及N文件数据块部分的行数。
假设最小值min是一万秒，当比min小时，记录新的min，并记下该数据块的位置i到n_epoch中
循环所有N文件中所有的数据块，返回最佳值

代码与解析

在程序设计时，将单次解算卫星位置的过程封装成一个函数，然后放入while循环中迭代计算，当信号传播时间收敛后，输出卫星位置结果。

定义一个结构体，用来当作函数的传参

//卫星位置传参
typedef struct Pos_t
{double X;double Y;double Z;double deltat;//改正前的接收机钟差double delta_t;//改正后的接收机钟差
}Pos_t;

#define C_V 299792458//光速（m）
#define GM 398600500000000//地心引力常数
#define math_e 2.718281828459 //e值
#define PI 3.141592653589793
#define Earth_e 7.2921151467e-5 //地球自转角速度
#define C1 4 //时间转换
double GPSsec = TimetoGPSsec(obs_e[i].y, obs_e[i].m, obs_e[i].d, obs_e[i].h, obs_e[i].min, obs_e[i].sec);
//根据O文件历元参考时间选择合适的N文件数据
int n_epoch = select_epoch(GPSsec, obs_e[i].sPRN[j], nav_b, n_n);
//观测时刻 - 参考时刻
double detat_toc = GPSsec - nav_b[n_epoch].TOE;
//计算近似的信号传播时间,接收机钟差已初始化为0(伪距/光速-接收机钟差+卫星钟差)
double delta_t = (obs_b[i].obs[j][C1] / C_V) - sta[i].delta_TR + nav_b[n_epoch].sa0 + nav_b[n_epoch].sa1 * detat_toc + nav_b[n_epoch].sa2 * pow(detat_toc, 2);
//计算卫星位置
double deltat = 0.0;//判断收敛
while (fabs(delta_t - deltat) > 0.0001)
{//临时结构体变量tmp，用来传参Pos_t tmp = { 0 };//计算卫星位置函数tmp = sat_pos(nav_b[n_epoch].deltan, nav_b[n_epoch].sqrtA, nav_b[n_epoch].TOE,nav_b[n_epoch].M0, nav_b[n_epoch].e, nav_b[n_epoch].omega, nav_b[n_epoch].OMEGA,nav_b[n_epoch].deltaomega, nav_b[n_epoch].Cuc, nav_b[n_epoch].Crc, nav_b[n_epoch].Cic,nav_b[n_epoch].Cus, nav_b[n_epoch].Crs, nav_b[n_epoch].Cis, nav_b[n_epoch].i0, nav_b[n_epoch].IDOT,delta_t, deltat, sta[i].X, sta[i].Y, sta[i].Z, GPSsec);//传参，更新信号传播时间deltat = tmp.deltat;delta_t = tmp.delta_t;sat[i][j].X = tmp.X;sat[i][j].Y = tmp.Y;sat[i][j].Z = tmp.Z;
}

其中：

obs_e：观测文件历元结构体，记录了每个观测值历元第一行时间及卫星数等信息
obs_b：观测文件数据块结构体，记录了每个观测历元观测值的数据
nav_b：导航文件数据块结构体，记录了每个历元的卫星参数
观测值文件和导航文件的读取可参考：RINEX O文件读取和RINEX N文件读取
detat_toc：计算卫星钟差所用的时间
delta_t：近似信号传播时间
obs_b[i].obs[j][C1] / C_V：表示第i个历元第j颗卫星的伪距值除以光速，C1和C_V为宏定义
sta[i].delta_TR：接收机钟差，i表示第i个历元，接收机钟差初始化时需为0
nav_b[n_epoch].sa0 + nav_b[n_epoch].sa1 * detat_toc + nav_b[n_epoch].sa2 * pow(detat_toc, 2)：该部分表示卫星钟差的计算，对照上文公式，省略了末项
deltat = 0.0：判断信号收敛，第一次计算时，需要初始化为0
Pos_t tmp：上文中用于传参的结构体
sat_pos：计算卫星位置函数，下文会详细展示

计算卫星位置函数

//计算卫星位置Pos_t sat_pos( double deltan,double sqrtA,double TOE,double M0,double e,double omega,double OMEGA,double deltaomega,double Cuc,double Crc, double Cic, double Cus,double Crs,double Cis,double i0,double IDOT,double delta_t, double deltat, double X_R,double Y_R, double Z_R, double GPSsec)
{Pos_t pos_t={0};//计算信号发射时刻=O文件观测时刻-信号传播时间double T_S = GPSsec - delta_t;//计算卫星的平均角速度ndouble n0 = sqrt(GM) / pow(sqrtA, 3);double n = n0 + deltan;//计算归划时间tkdouble tk = T_S - TOE;if (tk > 32400)tk -= 604800;//规划时间改正else if (tk < -32400)tk += 604800;//计算卫星发射时卫星的平近角Mdouble M = M0 + n * tk;//迭代计算偏近点角double E = M, E0;do{E0 = E;E = M + e * sin(E);} while (fabs(E - E0) > 1.0e-5);//计算真近点角Vdouble cosv = (cos(E) - e) / (1 - e * cos(E));//cosVdouble sinv = sqrt(1 - pow(e, 2)) * sin(E) / (1 - e * cos(E));//sinVdouble Vk = atan2(sinv, cosv);//注意atan与atan2的不同//计算升交角距udouble u = Vk + omega;//计算摄动改正项double Epsilon_u = Cuc * cos(2 * u) + Cus * sin(2 * u);double Epsilon_r = Crc * cos(2 * u) + Crs * sin(2 * u);double Epsilon_i = Cic * cos(2 * u) + Cis * sin(2 * u);//计算改正后的升交角距、轨道向径、轨道倾角double uk = u + Epsilon_u;double rk = pow(sqrtA, 2) * (1 - e * cos(E)) + Epsilon_r;double ik = i0 + Epsilon_i + IDOT * tk;//计算卫星在升交点轨道直角坐标系的坐标double xk = rk * cos(uk);double yk = rk * sin(uk);//计算升交点经度double L = OMEGA + (deltaomega - Earth_e) * tk - Earth_e * TOE; //计算卫星在地固系下的直角坐标double X = xk * cos(L) - yk * cos(ik) * sin(L);double Y = xk * sin(L) + yk * cos(ik) * cos(L);double Z = yk * sin(ik);//通过 Z 轴的旋转变换，对该坐标进行地球自转改正，得到新坐标pos_t.X = cos(Earth_e * delta_t) * X + sin(Earth_e * delta_t) * Y;pos_t.Y = -sin(Earth_e * delta_t) * X + cos(Earth_e * delta_t) * Y;pos_t.Z = Z;//重新计算信号传播的时间double R = sqrt(pow(X - X_R, 2) + pow(Y - Y_R, 2) + pow(Z - Z_R, 2));pos_t.deltat = delta_t;pos_t.delta_t = R / C_V;return pos_t;
}

（上述代码为了更加清晰的体现哪个是新变量、哪个是旧变量，将开辟变量的工作放在函数中间；读者自己写代码时，建议将开辟变量的工作统一放到函数的起始位置，增加运行效率；有些语言不支持程序运行后再开辟变量，例如：Fortran）

传入参数：从deltann到IDOT，均为N文件中读取的参数，delta_t和deltat为信号传播时间，用于判断信号传播时间是否收敛，X_R，Y_R，Z_R为测站坐标，首次迭代时，可初始化为0或概略坐标（O文件头），GPSsec为转化成GPS时的观测时刻

上述代码中有关时间的参数比较多，这里再次梳理一遍，防止混淆：

观测时刻（GPSsec）：接收机收到信号的时刻，O文件每个历元的第一行记录，需转换成GPS周内秒

卫星钟差时间（detat_toc）：由观测时刻减去卫星信号发射时刻TOE，TOE以GPS周内秒的形式存储，这个时间只用于卫星钟差改正

信号近似传播时间（delta_t）：由伪距进行计算，需要进行卫星钟差、接收机钟差、电离层和对流层改正（上述代码没有加入电离层和流层改正，推荐两种简单的改正模型：电离层经验模型Klobuchar，对流层经验模型GCAT）

信号发射时刻（T_S）：由观测时刻减去信号近似传播时间

规划时间（tk）：将信号发射时刻规划到以TOE为基准的时刻

上述代码与公式一一对应，需要注意以下几点：

1）if (tk > 32400)tk -= 604800;else if (tk < -32400)tk += 604800;规划时间改正，604800为一周的秒数，32400为一周半的秒数。该部分内容可参考其他博主：卫星发射时刻归化

2）计算偏近点角E时，因为E极小，迭代几次即可收敛，因此收敛条件只要保证精度即可,在计算卫星钟差时，末项的改正数用到了偏近点角E，如需改正，可将E保留进行传参

3）C语言中角度计算均是以弧度为单位；atan和atan2均是求反正切函数，后者的使用范围是是四象限角

4）上述中用到的sqrt，pow，fabs分别是：开方函数，幂函数，取绝对值函数，均需包含头文件

BDS卫星位置

BDS的卫星位置解算与GPS卫星有很大相似之处，其中MEO与IGSO卫星位置解算与GPS一致，GEO卫星从计算升交点赤经开始有所变化，在解算位置前，需要根据卫星的PRN号来判断卫星的种类，GEO计算公式如下（公式选自本科时期的论文，如有错误多多包涵）：

注意：（4-27）中-5°表示角度，为GEO卫星的倾角

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：XGBoost

下一篇：论文解读 | [CVPR2019] 基于自适应文本区域表示的任意形状场景文本检测

GPS卫星位置解算

基础原理

1）卫星位置解算流程

2）卫星有关参数

3）卫星位置计算过程

程序设计

数据预处理

1）GPS时转换(TimetoGPSsec)

2）选择最佳历元(select_epoch)

代码与解析

BDS卫星位置

相关内容

热门资讯