1：特性

二叉搜索树是具有以下性质的二叉树

• 若左子树不为空，则所有左子树的值都＜根节点的值

• 若右子树不为空，则所有右子树的值都＜根节点的值

• 左右子树都为二叉搜索树

2：接口

2.1：节点的定义

    templatestruct BSTreeNode{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_key(key),_left(nullptr),_right(nullptr){}};//默认public

struct的默认访问权限就是public。

2.2：插入

        bool Insert(const K& key){//空树if (_root == nullptr){_root = new Node(key);return true;//插入成功}else{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key)//小 走左{parent = cur;cur = cur->_left;}else if (cur->_key < key) //大 走右{parent = cur;cur = cur->_right;}else{return false;//相等插入失败}}cur = new Node(key);if (parent->_key > key){//是左节点parent->_left = cur;}else{//是右节点parent->_right = cur;}return true;//插入成功}

2.3：删除

删除分为3种情况。

2.3.1：删除节点的左节点为空

左节点为空，说明右节点存在。

删除的思路可以为：先定义2个节点指针，一个保存父亲，一个保存要删除的节点，遍历找到要删除的节点，左节点为空，如果该删除的节点为父亲的左节点，就让父亲的左指向删除节点的右节点。如果删除节点是父亲的右节点同理。

要注意如果删除节点为根节点root，因为root的父节点是空，所以不能进行空指针的链接，因此直接让root等于root的右节点（默认构造的时候root的左右就是空），也就是置空。

2.3.2：删除节点的右节点为空

右节点为空，说明左节点存在。

删除的思路可以为：先定义2个节点指针，一个保存父亲，一个保存要删除的节点，遍历找到要删除的节点，右节点为空，如果该删除的节点为父亲的左节点，就让父亲的左指向删除节点的左节点。如果删除节点是父亲的右节点同理。

要注意如果删除节点为根节点root，因为root的父节点是空，所以不能进行空指针的链接，因此直接让root等于root的左节点（默认构造的时候root的左右就是空），也就是置空。

2.3.3：删除节点的左右节点都不为空

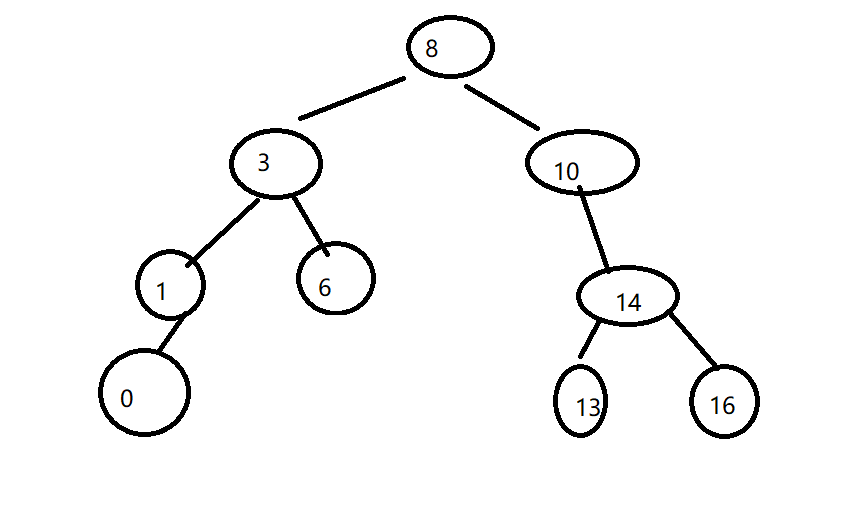
如图，如果需要删除8这个节点。

因为二叉搜索树的特性是，左子树各节点值必然小于根，右子树各节点值必然大于根。

删除8我们可以使用替换删除法。

2.3.3.1：替换删除法的思路

思路：定义2个指针，一个找合适的替换节点，一个找该合适节点的父亲节点。

找到后，将合适的替换节点值与删除节点值互换，delete合适的替换节点，再将替换节点的父亲节点与他的孩子节点链接。

下面是寻找合适替换节点的方法。

• 找到该节点左子树上的最大值（最右节点）替换，因为如果是从左子树去寻找合适的值，一定要满足左子树都小于这个替换后的值，也就是左子树上的最大值。因为右边必然大于左边和根，所以就是找该删除节点左子树上的最右值。

• 找到该节点右子树上的最小值（最左节点）替换，因为如果是从右子树去寻找合适的值，一定要满足右子树都大于这个替换后的值，也就是右子树上的最小值。因为左边必然小于右边和根，所以就是找该删除节点右子树上的最左值。

现在用右子树最小值替换删除节点，删除节点值已经变成了10，然后把替换节点的父亲与其孩子节点链接。此时只需要判断替换节点为父亲的左孩子还是右孩子，因为替换节点是在右子树找的最小节点，所以该替换节点必然不存在左节点（左子树必然小于根），所以就用父亲的左或者右链接该替换节点的右节点。

如果是用左子树的最大值替换删除节点，就是用父亲的左或者右去链接替换节点的左节点。

2.3.4：代码实现

        bool Insert(const K& key){//空树if (_root == nullptr){_root = new Node(key);return true;//插入成功}else{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key)//小 走左{parent = cur;cur = cur->_left;}else if (cur->_key < key) //大 走右{parent = cur;cur = cur->_right;}else{return false;//相等插入失败}}cur = new Node(key);if (parent->_key > key){//是左节点parent->_left = cur;}else{//是右节点parent->_right = cur;}return true;//插入成功}bool Erase(const K & key);{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){//走左parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//1:如果左为空//2:右为空//3:左右都不为空if (cur->_left == nullptr){//第一种情况左边为空//要让父亲链接自己，必须要确定自己是父亲的哪个节点，所以回头去写一个父亲指针//3种情况里面还有子情况，如果这个树只有一个节点，父节点就是空指针要单独考虑if (cur == _root){_root = cur->_right;//就是把root置空}else{if (parent->_left == cur){//左节点parent->_left = cur->_right;}else{//右节点parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){if (_root == cur){_root = cur->_left;}else{if (parent->_left == cur){//左节点parent->_left = cur->_left;}else{//右节点parent->_right = cur->_left;}}delete cur;}else{//用右子树最小的节点替换要删除的节点Node* parent = nullptr;Node* minright = cur->_right;while (minright->_left){parent = minright;minright = minright->_left;}cur->_key = minright->_key;//找右子树最小的//交换数值if (minright == parent->_left){parent->_left = minright->_right;//因为我已经是最小的了，你不可能链接到我的左节点这个比我还小的}else{parent->_right = minright->_right;}delete minright;}return true;}}return false;}}

因为递归需要建立大量栈帧（但是代码量较轻松），这里就只用循环写法。

2.4：中序遍历

中序遍历就是，依照左子树，根，右子树的遍历方式，可以得到一个升序的排序。

这里用递归较为简单。

        void _InorderR(Node* root){if (root == nullptr){return;}else{_InorderR(root->_left);cout << root->_key << " ";_InorderR(root->_right);}}

3：总结

二叉搜索树为了set和map做铺垫，后面还会学习到AVL树（高度平衡二叉搜索树）和红黑树。

搜索效率为log以2为底的N