本次实验大部分素材来源于山大王成优老师的讲义以及冈萨雷斯（MATLAB版），仅作个人学习笔记使用，禁止用作商业目的。

文章目录

• • 一、实验目的
  • 二、实验例题
  • • 1. 二维离散余弦变换(Discrete Cosine Transform, DCT)的基图像
    • 2. JPEG 压缩
    • • 2.1 DCT 和量化
      • 2.2 熵编码
      • • 2.2.1 AC 系数的 Huffman 编码
        • 2.2.2 DC 系数的 Huffman 编码
    • 3. 比特平面编码

一、实验目的

1. 掌握 DCT 变换的基图像画法。
2. 掌握 JPEG 压缩的整体框架及其实现程序。
3. 掌握比特平面编码方法。

二、实验例题

1. 二维离散余弦变换(Discrete Cosine Transform, DCT)的基图像

C(i,j)={1N,i=0,j=0,1,⋯,N−1,2Ncos⁡i(2j+1)π2N,i=1,2,⋯,N−1,j=0,1,⋯,N−1.\boldsymbol{C}(i, j)=\left\{\begin{array}{ll} \sqrt{\frac{1}{N}}, & i=0, j=0,1, \cdots, N-1, \\ \sqrt{\frac{2}{N}} \cos \frac{i(2 j+1) \pi}{2 N}, & i=1,2, \cdots, N-1, j=0,1, \cdots, N-1 . \end{array}\right. C(i,j)=⎩⎨⎧​N1​​,N2​​cos2Ni(2j+1)π​,​i=0,j=0,1,⋯,N−1,i=1,2,⋯,N−1,j=0,1,⋯,N−1.​
C=[β0Tβ1T⋮βN−1T]=[β0,0β0,1⋯β0,N−1β1,0β1,1⋯β1,N−1⋮⋮⋱⋮βN−1,0βN−1,1⋯βN−1,N−1]\boldsymbol{C}=\left[\begin{array}{c} \boldsymbol{\beta}_{0}^{\mathrm{T}} \\ \boldsymbol{\beta}_{1}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{\beta}_{N-1}^{\mathrm{T}} \end{array}\right]=\left[\begin{array}{cccc} \beta_{0,0} & \beta_{0,1} & \cdots & \beta_{0,N-1} \\ \beta_{1,0} & \beta_{1,1} & \cdots & \beta_{1,N-1} \\ \vdots & \vdots & \ddots & \vdots \\ \beta_{N-1,0} & \beta_{N-1,1} & \cdots & \beta_{N-1,N-1} \end{array}\right]C=​β0T​β1T​⋮βN−1T​​​=​β0,0​β1,0​⋮βN−1,0​​β0,1​β1,1​⋮βN−1,1​​⋯⋯⋱⋯​β0,N−1​β1,N−1​⋮βN−1,N−1​​​

Y=CXCT=[β0Tβ1T⋮βN−1T]X[β0,β1,⋯,βN−1]\boldsymbol{Y}=\boldsymbol{C X C}^{\mathrm{T}}=\left[\begin{array}{c} \boldsymbol{\beta}_{0}^{\mathrm{T}} \\ \boldsymbol{\beta}_{1}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{\beta}_{N-1}^{\mathrm{T}} \end{array}\right] \boldsymbol{X}\left[\boldsymbol{\beta}_{0}, \boldsymbol{\beta}_{1}, \cdots, \boldsymbol{\beta}_{N-1}\right]Y=CXCT=​β0T​β1T​⋮βN−1T​​​X[β0​,β1​,⋯,βN−1​]

式写成分量形式为
y(i,j)=∑r=0N−1∑k=0N−1βi,rβj,kx(r,k)=∑r=0N−1∑k=0N−1Bi,j(r,k)x(r,k)y(i, j)=\sum_{r=0}^{N-1} \sum_{k=0}^{N-1} \beta_{i, r} \beta_{j, k} x(r, k)=\sum_{r=0}^{N-1} \sum_{k=0}^{N-1} B_{i, j}(r, k) x(r, k) y(i,j)=r=0∑N−1​k=0∑N−1​βi,r​βj,k​x(r,k)=r=0∑N−1​k=0∑N−1​Bi,j​(r,k)x(r,k)

上面的推导可能一下子想不明白，我们可以依次进行，先求得X[β0,β1,⋯,βN−1]\boldsymbol{X}\left[\boldsymbol{\beta}_{0}, \boldsymbol{\beta}_{1}, \cdots, \boldsymbol{\beta}_{N-1}\right]X[β0​,β1​,⋯,βN−1​]的这个 N×NN\times NN×N 矩阵中第 j 列的值。

设 z(r,j)z(r,j)z(r,j) 为 X[β0,β1,⋯,βN−1]\boldsymbol{X}\left[\boldsymbol{\beta}_{0}, \boldsymbol{\beta}_{1}, \cdots, \boldsymbol{\beta}_{N-1}\right]X[β0​,β1​,⋯,βN−1​] 第 r 行，第 j 列的值。

Z=[x(0,0)x(0,1)⋯x(0,k)⋯x(0,N−1)x(1,0)x(1,1)⋯x(1,k)⋯x(1,N−1)⋮⋮⋱⋮⋱⋮x(r,0)x(r,1)⋯x(r,k)⋯x(r,N−1)⋮⋮⋱⋮⋱⋮x(N−1,0)x(N−1,1)⋯x(N−1,k)⋯x(N−1,N−1)][β0,0β1,0⋯βj,0⋯β0,N−1β0,1β1,1⋯βj,1⋯β1,N−1⋮⋮⋱⋮⋱⋮β0,N−1β1,N−1⋯βj,N−1⋯βN−1,N−1]\boldsymbol Z=\left[\begin{array}{cccc} x(0,0) & x(0,1)& \cdots & x(0,k) & \cdots & x(0,N-1) \\ x(1,0) & x(1,1) & \cdots & x(1,k) & \cdots & x(1,N-1) \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ x(r,0) & x(r,1) & \cdots & x(r,k) & \cdots & x(r,N-1) \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ x(N-1,0) & x(N-1,1) & \cdots & x(N-1,k) &\cdots & x(N-1,N-1) \end{array}\right] \left[\begin{array}{cccc} \beta_{0,0} & \beta_{1,0} & \cdots & \beta_{j,0} & \cdots & \beta_{0,N-1} \\ \beta_{0,1} & \beta_{1,1} & \cdots & \beta_{j,1} & \cdots & \beta_{1,N-1} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ \beta_{0,N-1} & \beta_{1,N-1} & \cdots & \beta_{j,N-1} &\cdots & \beta_{N-1,N-1} \end{array}\right]Z=​x(0,0)x(1,0)⋮x(r,0)⋮x(N−1,0)​x(0,1)x(1,1)⋮x(r,1)⋮x(N−1,1)​⋯⋯⋱⋯⋱⋯​x(0,k)x(1,k)⋮x(r,k)⋮x(N−1,k)​⋯⋯⋱⋯⋱⋯​x(0,N−1)x(1,N−1)⋮x(r,N−1)⋮x(N−1,N−1)​​​β0,0​β0,1​⋮β0,N−1​​β1,0​β1,1​⋮β1,N−1​​⋯⋯⋱⋯​βj,0​βj,1​⋮βj,N−1​​⋯⋯⋱⋯​β0,N−1​β1,N−1​⋮βN−1,N−1​​​

z(r,j)=∑k=0N−1x(r,k)βj,kz(r,j)=\sum_{k=0}^{N-1} x(r, k) \beta_{j, k}z(r,j)=k=0∑N−1​x(r,k)βj,k​

y(i,j)=∑r=0N−1βi,rz(r,j)=∑r=0N−1βi,r(∑k=0N−1x(r,k)βj,k)=∑r=0N−1∑k=0N−1βi,rβj,kx(r,k)=∑r=0N−1∑k=0N−1Bi,j(r,k)x(r,k)\begin{aligned} y(i, j) & =\sum_{r=0}^{N-1} \beta_{i, r} z(r, j) \\ & =\sum_{r=0}^{N-1} \beta_{i, r}\left(\sum_{k=0}^{N-1} x(r, k) \beta_{j, k}\right) \\ & =\sum_{r=0}^{N-1} \sum_{k=0}^{N-1} \beta_{i, r} \beta_{j, k} x(r, k)\\ &=\sum_{r=0}^{N-1} \sum_{k=0}^{N-1} B_{i, j}(r, k) x(r, k) \end{aligned}y(i,j)​=r=0∑N−1​βi,r​z(r,j)=r=0∑N−1​βi,r​(k=0∑N−1​x(r,k)βj,k​)=r=0∑N−1​k=0∑N−1​βi,r​βj,k​x(r,k)=r=0∑N−1​k=0∑N−1​Bi,j​(r,k)x(r,k)​

其中，CCC 的行向量的外积展开 Bi,j=βiβjT\boldsymbol{B}_{i, j}=\boldsymbol{\beta}_{i} \boldsymbol{\beta}_{j}^{\mathrm{T}}Bi,j​=βi​βjT​ 称为分解基图像。

者使用 MATLAB 函数 dctmtx 可得到 DCT 变
换矩阵，其一般语法为：
D = dctmtx (N);
其中，D 是 N×NN\times NN×N大小的 DCT 变换矩阵。

例 1 请画出 N=4N=4N=4 时 DCT 变换的基图像。

close all; clear all; clc;
A = dctmtx(4);
B = A';
C = zeros(4, 4, 16);
m = 0;
for i = 1:4for j = 1:4m = m+1;C(:, :, m) = B(:, i)*A(j, :);end
end
minvalue = min(min(min(C)));
maxvalue = max(max(max(C)));
figure,
for k = 1:16subplot(4, 4, k), imshow(C(:, :, k), [minvalue, maxvalue]);
end

ctrl+all 然后 ctrl+i 就可以格式化所有代码

2. JPEG 压缩

目前，最流行且最全面的连续色调静止图像压缩标准之一是 JPEG(JointPhotographic Experts Group，联合图像专家组)标准。在 JPEG 基准编码系统(该系统基于DCT变换，且对于大多数压缩应用来说是足够的)中，输入图像和输出图像均为8比特图像。基于 DCT 的 JPEG 标准的编解码框图如图所示。

编码器主要由 4 个部分组成：DCT 变换、量化、Zig-zag 扫描和熵编码。编码时，输入图像首先被分成 8×88\times 88×8的图像块，依次将每个图像块经过 DCT 变换为 64 个 DCT 系数，其中，最左上角的一个为直流系数(Direct Current, DC)，另外的 63 个系数称为交流系数(Alternating Current, AC)。量化后，对每个块的 DC 系数进行差分脉冲调制编码(Differential Pulse Code Modulation, DPCM)；其余 63 个 AC 系数经过 Zig-zag 扫描转变为一维序列，进行游程编码(Run Length Coding, RLC)，然后再对 DC 系数的差值和 AC 系数游程编码的码字进行基于统计特性的 Huffman 熵编码。

源图像数据取样值为无符号整数，取值范围为 [0,2P−1][0,2^P-1][0,2P−1]，其中 P 称为样值精度。对基于 DCT 的压缩编码，JPEG 定义两种可选的样值精度为 8 比特和 12 比特，基本系统采用 8 比特精度。

2.1 DCT 和量化

图像样值在 DCT 变换前，首先进行电平平移，通过减去 2P−12^{P-1}2P−1 变为带符号整数。电平平移的目的是为了降低 DCT 运算时的内部精度要求。图像样值经电平平移后，再按图 2 所示的光栅扫描顺序依次对
8×88\times 88×8 的数据块进行 DCT 变换。8×88\times 88×8 DCT 变换和反变换的数学公式分别如式(3)和式(4)所示。

F(u,v)=14C(u)C(v)[∑i=07∑j=07f(i,j)cos⁡(2i+1)uπ16cos⁡(2j+1)vπ16]F(u, v)=\frac{1}{4} C(u) C(v)\left[\sum_{i=0}^{7} \sum_{j=0}^{7} f(i, j) \cos \frac{(2 i+1) u \pi}{16} \cos \frac{(2 j+1) v \pi}{16}\right] F(u,v)=41​C(u)C(v)[i=0∑7​j=0∑7​f(i,j)cos16(2i+1)uπ​cos16(2j+1)vπ​]

f(i,j)=14[∑u=07∑v=07C(u)C(v)F(u,v)cos⁡(2i+1)uπ16cos⁡(2j+1)vπ16]f(i, j)=\frac{1}{4}\left[\sum_{u=0}^{7} \sum_{v=0}^{7} C(u) C(v) F(u, v) \cos \frac{(2 i+1) u \pi}{16} \cos \frac{(2 j+1) v \pi}{16}\right]f(i,j)=41​[u=0∑7​v=0∑7​C(u)C(v)F(u,v)cos16(2i+1)uπ​cos16(2j+1)vπ​]

其中, i,j,u,v=0,1,⋯,7,C(u),C(v)={1/2,u,v=01,其它 。 i, j, u, v=0,1, \cdots, 7, \quad C(u), C(v)=\left\{\begin{array}{ll} 1 / \sqrt{2}, & u, v=0 \\ 1, & \text { 其它 } \end{array}\right. \text { 。 }i,j,u,v=0,1,⋯,7,C(u),C(v)={1/2​,1,​u,v=0 其它 ​ 。 

量化过程是一个多对一的映射，因此该过程是有损压缩，它也是基于 DCT 的编码器信息损失的根源。量化定义为每一个 DCT 系数与它相对应的量化步长相除，并将所得的结果进行四舍五入取整。其公式为

Fquv=[FuvQuv]F_{q_{u v}}=\left[\frac{F_{u v}}{Q_{u v}}\right]Fquv​​=[Quv​Fuv​​]

其中，
FuvF_{u v}Fuv​ 和 FquvF_{q_{u v}}Fquv​​ 分别为量化前和量化后的 DCT 系数；QuvQ_{u v}Quv​ 为量化步长；[⋅][\cdot][⋅] 表示四舍五入取整。

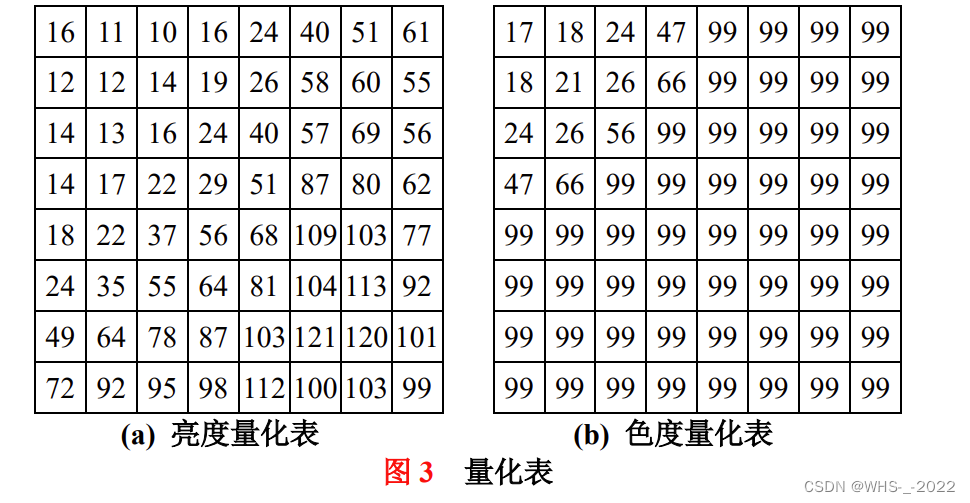
这个量化表右下角的数值较高，哪里有人眼不擅长感知的高频数据。

JPEG 建议采用图 3 给出的亮度和色度量化表，表中给出的量化步长是根据大量的主观实验确定的。64 个变换系数经量化后，DCT 系数矩阵变得稀疏。左上角系数是直流分量(DC 系数)。由于相邻 8×88\times 88×8 块之间的 DC 系数一般有很强的相关性，JPEG 并不直接对 DC 系数进行编码，而是采用 DPCM 编码，即对相邻两块 DC 系数的差值
DIFF=DCi−DCi−1\mathrm{DIFF}=\mathrm{DC}_{i}-\mathrm{DC}_{i-1}DIFF=DCi​−DCi−1​ ( iii 为块号)进行编码，如图 4 所示。而大部分位于矩阵右下角的高频分量(AC 系数)被量化为零。如图 5 所示，JPEG 中采用 Z 字形(Zig-zag)扫描方式将已量化的二维 DCT 系数变为一维序列，对连零的游程(数目)长度进行游程编码以代替逐个地传送这些零值，进一步实现数据压缩。当剩下的所有系数都为零时，用符号 EOB(End of Block) 来表示。

2.2 熵编码

熵编码属于无损编码，其目的是根据量化后 DCT 系数的统计特性进一步对图像数据进行压缩。JPEG 标准中定义了两种熵编码方法，即 Huffman 编码和算术编码。其中，JPEG 基本系统只采用 Huffman 编码。

2.2.1 AC 系数的 Huffman 编码

对 AC 系数进行 Huffman 编码时，Z 字形序列中每个非零 AC 系数和它前面的零游程(RUNLENGTH)一起被描述为如下的符号对：

                      符号 A                                        符号 B

                   (RUNLENGTH)                               (AMPLITUDE)

其中，符号 A 中的 RUNLENGTH 表示 Z 字形序列中被编码的非零 AC 系数前面连续为零的 AC 系数的数目；符号 B 中的 AMPLITUDE 为该非零 AC 系数的幅值；符号 A 中的 SIZE 则给出了用于编码表示 AMPLITUDE 所需的比特数。但由于 RUNLENGTH 只用于表示 0~15之间的零游程，而 Z 字形序列中实际的零游程可能大于 15，为此，JPEG 采用值为 (15,0)(15,0)(15,0) 的符号 A 来表示 RUNLENGTH＝16(ZRL)，在一个符号 A 前可以连续存在 3 个(15,0)这样的扩展符号，其后的符号 A 后面紧跟着一个符号 B。若最后的零游程包括尾块的 AC系数(即第 63 个 AC 系数)，此种情况下，采用值为(0,0)的符号 A 来表示块结束(EOB)。这样，每个 8×88×88×8 的 Z 字形序列中的 63 个 AC 系数就被转换成符号对 A,B 的序列；在零游程较长的情况下，符号 A 会连续出现在序列中；在 EOB 情况下，则只出现符号 A，后面不再会有符号 B。

对于基本系统，量化后 AC 系数的动态范围为[−210,210−1][-2^{10},2^{10}-1][−210,210−1]。因此，SIZE 的取值为 0~10 之间的整数，可以用 4 位二进制数表示； RUNLENGTH 的取值为 0~15 之间的整数，也可以用 4 位二进制数表示。

是有问题的， AC 系数的动态范围为[−210,210−1][-2^{10},2^{10}-1][−210,210−1]，那么如果 SIZE 的取值为 0~10 之间，是没办法表示正负值的，必须要有符号位。可后文中又说 VLI 码的最高位是从右边数第 SIZE 个比特，同时 MATLAB 代码中注释是反码，这里又说是 AMPLITUDE-1，十分的混乱。

后来我终于明白了，确实是只用 SIZE 表示的 AC 信号的幅值。比如如果是 1 的话，AMPLITUDE 只会是 1；但如果是 -6，它会用 001 来表示，如下图。这样就不会发生表示上的混乱。深蓝色是最基本的行程编码(RLE)，灰色是中间形式，也就是我们这里所提到的符号 A 和符号 B 的符号对。

实际操作时，JPEG 用一个复合的 8 比特RS=“RRRRSSSS”来表示符号 A。对于一个特定的非零 AC 系数，RS 中的低位“SSSS”用于表示 SIZE，高位“RRRR”则用于表示 RUNLENGTH。若 Z 字形序列中最后部分全为零，则使用 EOB 来标识块结束(在解码端根据该标志用零补齐 64 个系数)。图 6 所示为符号 A 的组成结构，其中 RS=“11110000”表示 RUNLENGTH＝16，RS=“00000000”表示 EOB，N/A 为未定义项。

JPEG 根据 Huffman 码表对符号 A 进行相应的 Huffman 编码，如表 1；对符号 B 则根据表 2 进行变字长整数(VLI)编码，而后将符号 B 的 VLI 码附加在符号 A 的 Huffman 码后，从而形成符号对 A,B 的最终编码结果。

对符号 B 中的 AMPLITUDE 进行变字长整数编码时，若 AMPLITUDE>0，相应的 VLI 码为 AMPLITUDE 二进制表示的低 SIZE 比特；若 AMPLITUDE<0，相应的 VLI 码则为(AMPLITUDE-1)二进制表示的的低 SIZE 比特。VLI 码的最高位(即从右数第 SIZE 个比特)代表 AMPLITUDE 的符号：0 为负值，1 为正值。VLI 虽是变字长码，但它不是 Huffman 码，两者的重要区别是，Huffman 码的码长直到解码时才能确定，而 VLI 码的长度却是存放在它前面用以表示符号 A 的Huffman 码中(这里，VLI 码的长度等于符号 A 中的 SIZE)。系统解码过程中，VLI 码可以通过计算得到，而不用像 Huffman 表那样存储起来。

这里的低 SIZE 比特表示为 AMPLITUDE 二进制表示之后，只取符号 A 当中的 SIZE 比特的二进制数据。我同时有几点困惑：① VLI 码的最高位表示 AMPLITUDE 的符号，但是 0 表示为负值，1 为正值 ② SIZE 是表示 AMPLITUDE 的符号位数的，那包不包括 AMPLITUDE 的符号位？③ 低 SIZE 比特是什么意思？

① 这是的符号位与 JPEG 这里特殊的变长编码有关。


② SIZE 既是符号位，同时也有对应的数值。


③ 字面意义理解，就是二进制表示的低 SIZE 位。这里“若 AMPLITUDE<0，相应的 VLI 码则为(AMPLITUDE-1)二进制表示的的低 SIZE 比特”，主要是因为默认的二进制表示是补码的形式，AMPLITUDE-1 即为反码的表示形式。

例 2 图 7 给出了一幅 Lena 图像，请使用上述 DCT-JPEG 压缩系统对其进行压缩，并求压缩比特率。

close all;clear all;clc;
I=imread('Lena512.bmp');%%读bmp灰度图像
figure,imshow(I,[]);
Q=1;%%设定量化因子OriginalImage=I;
OriginalImage=double(OriginalImage);%%图像数据类型转换
ImageSub=OriginalImage-128;%%电平平移128
[Row,Col]=size(OriginalImage);%%图像的大小
BlockNumber=Row*Col/64;%%8*8分块数%% dct2变换：把ImageSub分成8*8像素块，分别进行dct2变换，得变换系数矩阵Coef
Coef=blkproc(ImageSub,[8,8],'dct2(x)');%% 量化：用量化矩阵L量化Coef得CoefAfterQ
%% JPEG建议量化矩阵
L=Q*[16  11  10  16  24  40  51  6112  12  14  19  26  58  60  5514  13  16  24  40  57  69  5614  17  22  29  51  87  80  6218  22  37  56  68 109 103  7724  35  55  64  81 104 113  9249  64  78  87 103 121 120 10172  92  95  98 112 100 103  99]; 
CoefAfterQ=blkproc(Coef,[8,8],'round(x./P1)',L);%%向靠近的整数取整%% 把CoefAfterQ分成8*8的块得分块矩阵CoefBlock
m=0;
for row=1:Row/8for col=1:Col/8m=m+1;CoefBlock(:,:,m)=CoefAfterQ(((row-1)*8+1):(row*8),((col-1)*8+1):(col*8));end
end
m;%% 把量化后各个分块的DC系数存放到行矩阵DC中
DC(m)=0;
for i=1:mDC(i)=CoefBlock(1,1,i);
end
DC;%% 求由各个DC系数的差值组成的行矩阵DCdif
DCdif(BlockNumber)=0;
DCdif(1)=DC(1);
for i=2:BlockNumberDCdif(i)=DC(i)-DC(i-1);
end
DCdif;%% 用行矩阵DCdif中的差值替换原来系数矩阵CoefBlock中各个分块的DC系数
m=0;
for i=1:Row/8for j=1:Col/8m=m+1;CoefBlock(1,1,m)=DCdif(m);end
end
m;%% 把分块矩阵CoefBlock放到变换系数大矩阵CoefDCchanged中
n=0;
for row=1:Row/8for col=1:Col/8n=n+1;CoefDCchanged(((row-1)*8+1):(row*8),((col-1)*8+1):(col*8))=CoefBlock(:,:,n);end
end
n;%%**************************************************************************************************
%% 至此，完成了所有块中DC系数的替换（除第一个分块以外），为以后的DC系数差分编码做好了准备
%%**************************************************************************************************%%*********************** the first--end blocks ************************

Coef=blkproc(ImageSub,[8,8],'dct2(x)');

这行代码使用了MATLAB的blkproc函数，对一个名为ImageSub的矩阵进行了处理，将其分成 8×88\times 88×8 大小的块，然后对每个块应用了二维离散余弦变换（DCT），并将结果存储在名为Coef的新矩阵中。

具体而言，blkproc函数接受三个参数：输入矩阵、块大小以及应用于块的函数。在这里，ImageSub是输入矩阵，块大小为 8×88\times 88×8。'dct2(x)'是一个字符串参数，表示要应用的函数是二维离散余弦变换（DCT）函数。函数将以 8×88\times 88×8 大小的块作为参数进行调用，最后返回 8×88\times 88×8 的结果矩阵。

这个代码行的输出结果是一个与输入矩阵大小相同的矩阵Coef，其中每个 8×88\times 88×8 的块被DCT变换后的系数所替代，用于表示该块的频域信息。

t=zigzag(k);

这行代码使用了一个名为zigzag的函数，它将一个矩阵（或向量）展开成一个一维向量，按照蛇形顺序（Zig-Zag）排列。k是输入矩阵或向量。

在MATLAB中，zigzag函数是自定义函数，需要提供该函数的定义或者该函数来自某个toolbox或其他来源。通常情况下，zigzag函数用于对离散余弦变换（DCT）或其他变换后的矩阵进行压缩和编码。

该行代码的输出结果是一个按照蛇形顺序排列的一维向量t，其中包含了输入矩阵或向量k的所有元素，但是以蛇形顺序排列。这个向量通常用于数据压缩和编码的目的。

function zigzaged=zigzag(block);%%**********************************************************************%%
% % zigzaged=zigzag(block);
% % Input: block为8*8的矩阵
% % Output: zigzaged为按ZigZag顺序扫描后1*64的一维矩阵
% % 
% % 测试矩阵1,进行Zig-Zag扫描后的输出为zigzaged
% % block=[ 1  2  3  4  5  6  7  8;
% %     9 10 11 12 13 14 15 16;
% %     17 18 19 20 21 22 23 24;
% %     25 26 27 28 29 30 31 32;
% %     33 34 35 36 37 38 39 40;
% %     41 42 43 44 45 46 47 48;
% %     49 50 51 52 53 54 55 56;
% %     57 58 59 60 61 62 63 64 ];
% % zigzaged=[1,2,9,17,10,3,4,11,18,25,33,26,19,12,5,6,13,20,27,34,41,49,42,35,28,21,14,7,...
% %     8,15,22,29,36,43,50,57,58,51,44,37,30,23,16,24,31,38,45,52,59,60,53,46,39,32,...
% %     40,47,54,61,62,55,48,56,63,64];
%%**********************************************************************%%% zigzaged=zigzag(reshape([1:64],8,8));zzscan=[1,2,9,17,10,3,4,11,18,25,33,26,19,12,5,6,13,20,27,34,41,49,42,35,28,21,14,7,...8,15,22,29,36,43,50,57,58,51,44,37,30,23,16,24,31,38,45,52,59,60,53,46,39,32,...40,47,54,61,62,55,48,56,63,64];
block1d=reshape(block',1,64);
zigzaged=block1d(zzscan);

这段代码是一个MATLAB函数，函数名为zigzag。它的输入是一个8x8的矩阵block，输出是一个按照Zig-Zag顺序扫描后的1x64的一维矩阵zigzaged。

该函数的实现过程是先定义了一个Zig-Zag扫描的顺序zzscan，然后将输入矩阵block转置后展开成一个1x64的一维矩阵block1d，最后按照Zig-Zag顺序将block1d的元素放到zigzaged中。

2.2.2 DC 系数的 Huffman 编码

由于亮度分量和色度分量的统计特性不同，它们的 Huffman 编码表也不同。相邻两块 DC 系数的差值(DIFF)描述为如下的符号对：
                      符号 A                                        符号 B

                      (SIZE)                                     (AMPLITUDE)

其中，符号 B 的 AMPLITUDE 为 DIFF 的幅值；符号 A 中的 SIZE 则给出了用于编码表示 DIFF 所需的比特数。由于 DIFF 的动态范围为 [−211,211−1][-2^{11},2^{11}-1][−211,211−1]，因此 SIZE 的取值为 0~11之间的整数。类似于 AC 系数编码，JPEG 对符号 A 根据相应的 Huffman 码表进行变字长编码，如表 3 所示；对符号 B 则根据表 2 进行 VLI 编码，而后将符号 B 的 VLI 码附加在符号 A 的 Huffman 码后，从而完成对 DIFF 的熵编码。

function [bit_seq,len]=DCHuffmanEncoding(x)%%****************************************************************
%% 对扫描后每块的DC系数差值进行Huffman编码
%% x为DC系数的差值
%%****************************************************************%%*********************************** DC Huffman Code Look up *********************************%%
%% val为x的绝对值，即幅度大小
%% dccode为用十进制数表示的编码结果，codelen为编码后的码长
%% 若x > 0，则用其二进制原码表示，若x < 0，则用其二进制反码表示，amplen为表示幅度所需的bit数
%%*********************************************************************************************%%
v0=x;
val=abs(x);
if (val==0);amplen=1;codelen=2;dccode=0;%% dccode=00
elseif(val==1);amplen=1;codelen=3;dccode=2;%% dccode=010
elseif(val >=    2 & val <=    3);amplen= 2;codelen = 3;dccode=  3;  %% dccode=011;
elseif(val >=    4 & val <=    7);amplen= 3;codelen = 3;dccode=  4;  %% dccode=100;
elseif(val >=    8 & val <=   15);amplen= 4;codelen = 3;dccode=  5;  %% dccode=101;
elseif(val >=   16 & val <=   31);amplen= 5;codelen = 3;dccode=  6;  %% dccode=110;
elseif(val >=   32 & val <=   63);amplen= 6;codelen = 4;dccode= 14;  %% dccode=1110;
elseif(val >=   64 & val <=  127);amplen= 7;codelen = 5;dccode= 30;  %% dccode=1 1110;
elseif(val >=  128 & val <=  255);amplen= 8;codelen = 6;dccode= 62;  %% dccode=11 1110;
elseif(val >=  256 & val <=  511);amplen= 9;codelen = 7;dccode=126;  %% dccode=111 1110;
elseif(val >=  512 & val <= 1023);amplen=10;codelen = 8;dccode=254;  %% dccode=1111 1110;
elseif(val >= 1024 & val <= 2047);amplen=11;codelen = 9;dccode=510;  %% dccode=1 1111 1110;
end
if v0>0 ;bit_seq=[dec2bin(dccode,codelen),dec2bin(val,amplen)];
else  bit_seq=[dec2bin(dccode,codelen),dec2bin(bitcmp(val,'int16'),amplen)];
end
len = numel(bit_seq);%% dec2bin()为十进制数到二进制数的转换，第一个参数是要转换的十进制数，
%% 第二个参数为转换后二进制码的位数（如果要求的位数大于直接转换后的位数，自动在前面补0）
%% bitcmp()取反码，第一个参数是要取反的二进数的十进制数表示，
%% 第二个参数指明对多少位的二进制数取反（如果要求的位数大于直接表示的二进制数的位数，自动在前面补0）
%% bitcmp()的结果为取反后的十进制数表示

dec2bin(dccode,codelen)

dec2bin(dccode,codelen) 是MATLAB的一个函数调用，用于将十进制整数 dccode 转换为 codelen 位的二进制字符串。其中，dccode 是需要转换的十进制整数，codelen 是期望输出的二进制字符串长度。函数返回一个字符串，表示 dccode 的二进制表示。如果二进制字符串的位数少于 codelen，则在字符串的左侧补 0 直至满足期望长度。

if v0>0 ;bit_seq=[dec2bin(dccode,codelen),dec2bin(val,amplen)];

例如，如果 dccode 的二进制编码是 “100”，val 的二进制编码是 “0101”，则 bit_seq 将是一个长度为 7 的字符向量，即 bit_seq = ['1000101']。

bitcmp(val,'int16')

bitcmp(val, 'int16')是一个MATLAB函数，用于将val的每个二进制位取反，并返回取反后的值。 ‘int16’ 是一个可选参数，表示将val转换为16位的有符号整数。如果省略此参数，则bitcmp默认使用class(val)的数据类型。

以下是一个例子：

x = 5; % 十进制整数5的二进制表示是101
y = bitcmp(x, 8); % 对5进行取反操作，由于5的二进制表示是101，所以取反之后的结果为010，将这个结果转换为十进制数值得到2

在这个例子中，变量 x 的值是十进制整数 5。当我们对 x 进行 bitcmp(x, 8) 操作时，函数将对 x 的二进制表示的每一位进行操作，对于二进制数值的每一位，取反之后得到的结果将作为新的数值的该位的值。由于 5 的二进制表示是 101，所以取反之后的结果是 010，这个结果对应的十进制整数是 2，所以最后变量 y 的值是 2。

直流系数差值编码规则是一种特殊的霍夫曼编码，用于对JPEG压缩图像的直流系数差值进行编码。以下是直流系数差值进行霍夫曼编码的规则：

1. 计算每个直流系数差值的幅值大小 val，即直流系数差值的绝对值。

2. 根据幅值大小 val 确定每个直流系数差值的霍夫曼编码值。这实际上是对 DC 系数的符号 A 进行编码。

• 若 val == 0，则编码值为 00。
• 若 val == 1，则编码值为 010。
• 若 2 <= val <= 3，则编码值为 011。
• 若 4 <= val <= 7，则编码值为 100。
• 若 8 <= val <= 15，则编码值为 101。
• 若 16 <= val <= 31，则编码值为 110。
• 若 32 <= val <= 63，则编码值为 1110。
• 若 64 <= val <= 127，则编码值为 1 1110。
• 若 128 <= val <= 255，则编码值为 11 1110。
• 若 256 <= val <= 511，则编码值为 111 1110。
• 若 512 <= val <= 1023，则编码值为 1111 1110。
• 若 1024 <= val <= 2047，则编码值为 1 1111 1110。

3. 对于直流系数差值为正数的情况，使用原码表示 B；对于直流系数差值为负数的情况，使用反码表示 B 的编码值。（通常这会导致正数以 1 开头，负数以 0 开头）

4. 将 SIZE 编码值和幅值 AMPLITUDE 分别写成二进制数，并将它们连接在一起，形成该直流系数差值的霍夫曼编码。编码 A 在前面，B 在后面。

实际上我就是对符号 A，也就是 SIZE 先进行了Huffman 编码，然后我再对符号 B，也就是 APMLITUDE 进行 VLI 编码。VLI 编码的含义就是，如果我 AMPLITUDE 在某个范围之内，我就用 SIZE 长度的二进制序列表示。合起来就是DC系数的 Huffman 编码。

3. 比特平面编码

一幅 m 比特单色图像的灰度，可以用如式(6)所示的基 2 多项式来表示：
am−12m−1+am−22m−2+⋯+a121+a020(6)a_{m-1} 2^{m-1}+a_{m-2} 2^{m-2}+\cdots+a_{1} 2^{1}+a_{0} 2^{0}\tag6 am−1​2m−1+am−2​2m−2+⋯+a1​21+a0​20(6)
基于这种特性，将该图像分解为二值图像集的一种简单方法是，把该多项式的 m 个系数分离为 m 个 1 比特的比特平面。结合教材 P70-71 理解。最低阶比特平面(对应最低阶比特的平面)是通过收集每个像素的 a0a_0a0​ 比特生成的，而最高阶比特平面包含 am−1a_{m-1}am−1​ 比特或系数。

这种分解方法的固有缺点是，灰度的较小变化会对比特平面的复杂性产生明显影响。例如，若一个灰度为 127(01111111) 的像素与一个灰度为 128(10000000) 的像素相邻，每个比特平面将包含一个对应 0 到 1(或 1 到 0)的转换。

一种替代分解方法(降低较小灰度变化带来的影响)是，首先用一个 mmm 比特格雷码表示图像。对应于式(6)(6)(6)中多项式的 mmm 比特格雷编码 gm−1⋯g2g1g0g_{m-1} \cdots g_{2} g_{1} g_{0}gm−1​⋯g2​g1​g0​ 可由式 (7)(7)(7) 计算得到：

gi=ai⊕ai+1,0≤i≤m−2gm−1=am−1(7)\begin{array}{l} g_{i}=a_{i} \oplus a_{i+1}, 0 \leq i \leq m-2 \\ g_{m-1}=a_{m-1} \end{array}\tag7 gi​=ai​⊕ai+1​,0≤i≤m−2gm−1​=am−1​​(7)

其中，⊕\oplus⊕ 表示异或运算。这种编码的唯一特性是连续码字只有 1 比特位不同。因此，较小的灰度变化不太能影响所有 mmm 个比特平面。例如，当灰度级 127 和 128 相邻时，只有最高阶比特平面包含有一个 0 到 1 的转换，因为对应于 127 和 128 的格雷码分别是
01000000 和 11000000。

使用函数 bitget 可获得指定数据位的值，其一般语法为：
C = bitget(A, BIT);

其中，A 为有符号或无符号的整数阵列，bitget 先将 A 转化成二进制序列，然后从右往左取第 BIT 位的值。

使用函数 bitxor 可实现数据位异或运算，其一般语法为：
C = bitxor(A, B);

其中，A 和 B 是有符号或无符号的整型数组，C 为返回的 A 和 B 按位异或的结果