数位dp-- 数字游戏_资讯

数位dp-- 数字游戏

创始人

2024-05-30 21:35:04

0次

题目

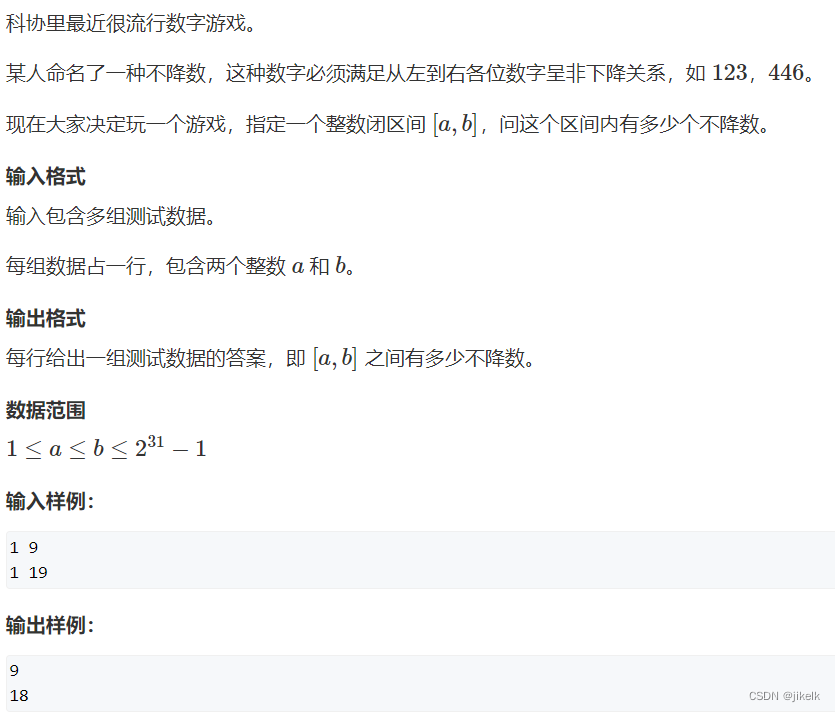
在这里插入图片描述
思路
也是一道比较典型的数位dp的问题，关键的思想跟我上一篇博客很像，
首先把区间值变成[1,Y]-[1,X-1]的值，然后单独计算得到结果。
总的来说就是把这个数的每一位都单独拿出来，然后根据选0-a_n-1和选**a_n**两种方案单独计算：

当选第一种方案时，就是后面的i位**（因为最低为从a₀开始）的数字可以任意选，那么就可以表示为前面的最高位为last**，一共i+1位的决策数。

ps：上一篇博客的图（

那么这里求决策数就需要用到动态规划了。
这里用f[i][j]表示前面的最高位为j，并且一共有i位的不降数的集合，
那么f[i][j]肯定要从前面的状态中得到，那么在第i位为j的时候，
i-1位的选择可以为 j , j + 1 , j + 2 ，… ， 9这些情况，
这些情况之和就相当于f[ i ] [ j ] , 那么f [ i ] [ j ]就可以表示为f[ i -1] [ j ]+f [ i-1 ] [ j + 1 ]+…+f [ i -1] [ 9 ]。这里可以预处理获得所有情况的f[ i ] [ j ]，这样上面的方案数就可以直接算出来了（这里借用了y总的图片一用）
在这里插入图片描述
当选第二种方案时
即要选择当前位的最大值时，要进行特判，即上一位的最大值是不是小于当前位的最大值的，（即last。然后走到最右下角的决策时如果还是能选到a₀，那么就作为一种方案数使res++，然后返回res即可。

具体代码

#include #include #include #include #include #include #include #include #include #define sc_int(x) scanf("%d", &x) #define sc_ll(x) scanf("%lld", &x) #define pr_ll(x) printf("%lld", x) #define pr_ll_n(x) printf("%lld\n", x) #define pr_int_n(x) printf("%d\n", x) #define ll long long using namespace std;const int N=20; int n ,m,h; int s[N][N];void cal() {for(int i =0;i<=9;i++)s[1][j]=1;for(int i =1;i<=N;i++)for(int j =0;j<=9;j++)for(int k=j;k<=9;k++)s[i][j]+=s[i-1][k]; }int dp(int n) {if(!n) return 1;//特判，如果为0也可以作为一种决策vectorcnt;while(n)cnt.push_back(n%10),n/=10;int res=0;int last=0;for(int i =cnt.size()-1;i>=0;i--){int x=cnt[i];for(int j =last;jx)break;x=last;if(!i)res++;}return res; } int main() {int t;cal();int l,r;while(cin>>l>>r)cout<
ps：作为数位dp的第二篇，感觉理解起来容易了很多（最不好理解的点还是方案数的预处理哪里），希望以后的数位dp能越学越熟悉吧。

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。上一篇：03_Linux压缩解压,用户用户组,文件权限下一篇：【JDK14 新特性】Record 相关内容

热门资讯运动会加油稿秋季运动会加油稿【秋季】　　让我们把全部的期待融入文字中，让我们用声音表达我们的热情，下面是关于秋季运动... 四个太阳说课稿四个太阳说课稿（精选5篇）　　作为一位兢兢业业的人民教师，有必要进行细致的说课稿准备工作，编写说课稿... 六年级语文《明天我们毕业了》... 苏教版六年级语文《明天我们毕业了》说课稿范文　　一、谈话导入　　1、同学们，不久你们就要小学毕业了，... 春的朗诵稿关于春的朗诵稿(3篇)　　随着社会不断地进步，大家都接触过朗诵稿吧，朗诵是用响亮有力的声音把文章背出... 中班夏天的雷雨说课稿中班夏天的雷雨说课稿　　作为一名中班的老师，我们知道开新课的时候知道怎么样书写好自己的说课稿吗？以下... 《心中的红领巾》说课稿四年级少先队活动课《心中的红领巾》说课稿范文　　在教学工作者实际的教学活动中，时常需要用到说课稿，借... 《北京亮起来了》说课稿《北京亮起来了》说课稿范文各位老师，今天我说课的内容是：　　一、教材的理解　　九年义务教育六年制小学... 小学数学四年级上册说课稿《找... 小学数学四年级上册说课稿《找规律》　　小学数学四年级上册说课稿《找规律》怎么写好呢?下面是由应届毕业... 七彩蝴蝶的说课稿七彩蝴蝶的说课稿　　一、说教材　　《七彩蝴蝶》是全国义务教育课程标准试验教科书小学二年级《艺术》（下... 《比热容》说课稿《比热容》说课稿《比热容》说课稿1　　一、说教材　　（一）教材的特点　　“比热容”是义教初中物理第二... 《寂寞的月亮》说课稿《寂寞的月亮》说课稿各位评委老师：　　上午好！我今天说课的题目是《寂寞的月亮》，下面我将从说教材、说... 家长会教师经典发言稿家长会教师经典发言稿　　一、家长会的形式　　1、发布会形式　　针对一项或多项主题，以教师讲述和传达为... 四年级上册《可能性》说课稿四年级上册《可能性》说课稿3篇　　说课，就是教师备课之后讲课之前（或者在讲课之后）把教材、教法、学法... 图形与变换复习小学数学说课稿图形与变换复习小学数学说课稿　　【教学内容】　　《义务教育课程标准实验教科书·数学》六年级下册第10... 1000米运动会加油稿　　一圈有一圈的坚持，是运动员的最可贵的精神，下面为大家带来的是1000米运动会加油稿范文，欢迎阅读... 语文质量分析会发言稿语文质量分析会发言稿（通用10篇）　　在日新月异的现代社会中，发言稿的使用越来越广泛，发言稿是在一定... 语文《恐龙的灭绝》说课稿语文《恐龙的灭绝》说课稿　　在教学工作者开展教学活动前，就有可能用到说课稿，借助说课稿可以有效提升自... 通讯稿通讯稿（精选19篇）　　在发展不断提速的社会中，我们需要用到通讯稿的情形越来越多，以下是小编为大家整... 语言欣赏《耳朵上的绿星》中班... 语言欣赏《耳朵上的绿星》中班说课材料　　一、说教材。　　（一）说设计意图：　　《耳朵上的绿星》这一内... 感恩国旗下讲话稿感恩国旗下讲话稿（通用5篇）　　随着社会一步步向前发展，用到讲话稿的地方越来越多，讲话稿是讲话者为了...