值函数近似

• Value Function Approximation
• • Motivating examples: curve fitting
  • Algorithm for state value estimation
  • • Objective function
    • Optimization algorithms
    • Selection of function approximators
    • Illustrative examples
    • Summary of the story
    • Theoretical analysis
  • Sarsa with function appriximation
  • Q-learning with function approximation
  • Deep Q-learning
  • 内容来源

Value Function Approximation

Motivating examples: curve fitting

到目前为止，我们都是使用tables表示state和action values。例如，下表是action value的表示：

• 优势：直观且容易分析
• 劣势：难以处理较大或者连续的state或者action空间。两个方面：1）存储；2）泛化能力。

举个例子：假定有一个one-dimensional states s1,...,s∣S∣s_1,...,s_{|S|}s1​,...,s∣S∣​，当π\piπ是给定策略的时候，它们的state values是vπ(s1),...,vπ(s∣S∣)v_\pi(s_1),...,v_\pi(s_{|S|})vπ​(s1​),...,vπ​(s∣S∣​)。假设∣S∣|S|∣S∣非常大，因此我们希望用一个简单的曲线近似它们的点以降低内存：

答案是可以的。
首先我们使用简单的straight line去拟合这些点。假设straight line的方程为

其中：

• www是参数向量（parameter vector）
• ϕ(s)\phi(s)ϕ(s)是s的特征向量（feature vector）
• v^(s,w)\hat{v}(s,w)v^(s,w)与www成线性关系（当然，也可以是非线性的）

这样表示的好处是：

• 表格形式需要存储∣S∣|S|∣S∣个state values，现在，只需要存储两个参数aaa和bbb
• 每次我们想要使用s的值，我们可以计算ϕT(s)w\phi^T(s)wϕT(s)w。
• 但是这个好处也不是免费的，它需要付出一些代价：state values不能被精确地表示，这也是为什么这个方法被称为value approximation。

既然直线不够准确，那么是否可以使用高阶的曲线呢？当然可以。第二，我们使用一个second-order curve去拟合这些点：

在这种情况下：

• www和ϕ(s)\phi(s)ϕ(s)的维数增加了，但是values可以被拟合的更加精确。
• 尽管v^(s,w)\hat{v}(s,w)v^(s,w)与sss是非线性的，但是它与www是线性的。这种非线性的性质包含在ϕ(s)\phi(s)ϕ(s)中。

当然，还可以继续增加阶数。第三，使用一个更加high-order polynomial curves（多项式曲线）或者其他复杂的曲线来拟合这些点：

• 好处是：更好的approximate
• 坏处是：需要更多的parameters

小结一下：

• Idea：value function approximation的idea是用一个函数v^(s,w)\hat{v}(s, w)v^(s,w)来拟合vπ(s)v_\pi(s)vπ​(s)，这个函数里边有参数www，所以被称为parameterized function，www就是parameter vector。
• 这样做的好处：
  • 1）节省存储：www的维数远小于∣S∣|S|∣S∣
  • 2）泛化能力：当一个state sss是visited，参数www是updated，这样某些其他unvisited states的values也可以被updated。按这种方式，the learned values可以泛化到unvisited states。

Algorithm for state value estimation

Objective function

首先，用一种更正式的方式：

• 令vπ(s)v_\pi(s)vπ​(s)和v^(s,w)\hat{v}(s,w)v^(s,w)分别表示true state value和approximate函数.
• 我们的目标是找到一个最优的www，使得v^(s,w)\hat{v}(s,w)v^(s,w)对于每个sss达到最优的近似vπ(s)v_\pi(s)vπ​(s)
• 这个问题就是一个policy evaluation问题，稍后我们将会把它推广到policy improvement。
• 为了找到最优的www，我们需要两步：
  • 第一步定义一个目标函数（object function）
  • 第二步是优化这个目标函数。

The objective function is:J(w)=E[(vπ(S)−v^(S,w))2]J(w)=\mathbb{E}[(v_\pi(S)-\hat{v}(S,w))^2]J(w)=E[(vπ​(S)−v^(S,w))2]

• 我们的目标是找到最优的www，这样可以最小化J(w)J(w)J(w)
• The expectation is with respect to the random variable S∈SS\in \mathcal{S}S∈S。SSS的概率分布是什么？
  • This is often confusing because we have not discussed the probability distribution of states so far
  • There are several ways to define the probability distribution of SSS.

第一种方式是使用一个uniform distribution.

• 它对待每个states都是同等的重要性，通过将每个state的概率设置为1/∣S∣1/|\mathcal{S}|1/∣S∣
• 这种情况下，目标函数变为：J(w)=E[(vπ(S)−v^(S,w))2]=1∣S∣∑s∈S(vπ(s)−v^(s,w))2J(w)=\mathbb{E}[(v_\pi (S)-\hat{v}(S,w))^2]=\frac{1}{|\mathcal{S}|}\sum_{s\in \mathcal{S}}(v_\pi(s)-\hat{v}(s,w))^2J(w)=E[(vπ​(S)−v^(S,w))2]=∣S∣1​s∈S∑​(vπ​(s)−v^(s,w))2
• 虽然平均分布是非常直观的，但是有一个问题：这里假设所有状态都是平等的，但是实际上可能不是那么回事。例如，某些状态在一个策略下可能几乎不会访问到。因此这种方式没有考虑一个给定策略下Markov process的实际动态变化。

第二种方式是使用stationary distribution

• Stationary distribution is an important concept. 它描述了一个Markov process的long-run behavior。
• 令{dπ(s)}s∈S\{d_\pi(s)\}_{s\in \mathcal{S} }{dπ​(s)}s∈S​表示基于策略π\piπ的Markov process的stationary distribution。根据定义有，dπ(s)≥0d_\pi(s)\ge 0dπ​(s)≥0且∑s∈Sdπ(s)=1\sum_{s\in \mathcal{S}}d_\pi(s)=1∑s∈S​dπ​(s)=1
• 在这种情况下，目标函数被重写为：J(w)=E[(vπ(S)−v^(S,w))2]=∑s∈Sdπ(s)(vπ(s)−v^(s,w))2J(w)=\mathbb{E}[(v_\pi (S)-\hat{v}(S,w))^2]=\sum_{s\in \mathcal{S}}d_\pi (s)(v_\pi(s)-\hat{v}(s,w))^2J(w)=E[(vπ​(S)−v^(S,w))2]=s∈S∑​dπ​(s)(vπ​(s)−v^(s,w))2这里的dπ(s)d_\pi(s)dπ​(s)就扮演了权重的意思，这个函数是一个weighted squared error。
• 由于更频繁地visited states，具有更高的dπ(s)d_\pi(s)dπ​(s)值，它们在目标函数中的权重也比那些很少访问的states的权重高。

对于stationary distribution更多的介绍：

• Distribution：state的Distribution
• Stationary : Long-run behavior
• Summary: 智能体agent根据一个策略运行一个较长时间之后，the probability that the agent is at any state can be described by this distribution.

需要强调的是：

• Stationary distribution 也被称为steady-state distribution，或者limiting distribution
• 它在理解value functional approximation method方面是非常重要的
• 对于policy gradient method也是非常重要的。

举个例子：如图所示，给定一个探索性的策略。让agent从一个状态出发然后跑很多次，根据这个策略，然后看一下会发生什么事情。

• 令nπ(s)n_\pi(s)nπ​(s)表示次数，sss has been visited in a very long episode generated by π\piπ。
• 然后，dπ(s)d_\pi(s)dπ​(s)可以由下式估计：dπ(s)≈nπ(s)∑s′∈Snπ(s′)d_\pi(s)\approx \frac{n_\pi(s)}{\sum_{s'\in \mathcal{S}}n_\pi(s') }dπ​(s)≈∑s′∈S​nπ​(s′)nπ​(s)​
  
  The converged values can be predicted because they are the entries of dπd_\pidπ​：dπT=dπTPπd_\pi^T=d_\pi^TP_\pidπT​=dπT​Pπ​
  对于上面的例子，有PπP_\piPπ​：Pπ=[0.30.10.600.10.300.60.100.30.600.10.10.8]P_\pi=\begin{bmatrix}0.3 & 0.1 & 0.6 & 0\\0.1 & 0.3 & 0 & 0.6\\0.1 & 0 & 0.3 & 0.6\\0 & 0.1 & 0.1 & 0.8\end{bmatrix}Pπ​=​0.30.10.10​0.10.300.1​0.600.30.1​00.60.60.8​​可以计算出来它左边对应于eigenvalue等于1的那个eigenvector：dπ=[0.0345,0.1084,0.1330,0.7241]Td_\pi=[0.0345, 0.1084, 0.1330, 0.7241]^Tdπ​=[0.0345,0.1084,0.1330,0.7241]T

Optimization algorithms

当我们有了目标函数，下一步就是优化它。为了最小化目标函数J(w)J(w)J(w)，我们可以使用gradient-descent算法：wk+1=wk−αk∇wJ(wk)w_{k+1}=w_k-\alpha_k\nabla_w J(w_k)wk+1​=wk​−αk​∇w​J(wk​)它的true gradient是：

这个true gradient需要计算一个expectation。我们可以使用stochastic gradient替代the true gradient：wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t (v_\pi(s_t)-\hat{v}(s_t,w_t))\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​(vπ​(st​)−v^(st​,wt​))∇w​v^(st​,wt​)其中sts_tst​是S\mathcal{S}S的一个采样。这里2αk2\alpha_k2αk​合并到了αk\alpha_kαk​。

• 这个算法在实际当中是不能使用的，因为它需要true state value vπv_\pivπ​，这是未知的。
• 可以使用vπ(st)v_\pi(s_t)vπ​(st​)的一个估计来替代它，这样该算法就可以实现了

那么如何进行代替呢？有两种方法：

• 第一种，Monte Carlo learning with function approximation
  令gtg_tgt​表示在episode中从sts_tst​开始的discounted return，然后使用gtg_tgt​近似vπ(st)v_\pi(s_t)vπ​(st​)。该算法变为wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t (g_t-\hat{v}(s_t,w_t))\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​(gt​−v^(st​,wt​))∇w​v^(st​,wt​)
• 第二种，TD learning with function approximate
  By the spirit of TD learning, rt+1+γv^(st+1,wt)r_{t+1}+\gamma \hat{v}(s_{t+1}, w_t)rt+1​+γv^(st+1​,wt​)可以视为vπ(st)v_\pi(s_t)vπ​(st​)的一个近似。因此，算法变为：wt+1=wt+αt[rt+1+γv^(st+1,wt)]∇wv^(st,wt)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \hat{v}(s_{t+1}, w_t)]\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​[rt+1​+γv^(st+1​,wt​)]∇w​v^(st​,wt​)

TD learning with function approximation的伪代码：

该方法仅能估计在给定policy情况下的state values，但是对于后面的算法的理解是非常重要的。

Selection of function approximators

如何选取函数v^(s,w)\hat{v}(s,w)v^(s,w)？

• 第一种方法，也是之前被广泛使用的，就是linear functionv^(s,w)=ϕT(s)w\hat{v}(s,w)=\phi^T(s)wv^(s,w)=ϕT(s)w这里的ϕ(s)\phi(s)ϕ(s)是一个feature vector， 可以是polynomial basis，Fourier basis,…。
• 第二种方法是，现在广泛使用的，就是用一个神经网络作为一个非线性函数近似器。神经网络的输入是state，输出是v^(s,w)\hat{v}(s,w)v^(s,w)，网络参数是www。

在线性的情况中v^(s,w)=ϕT(s)w\hat{v}(s,w)=\phi^T(s)wv^(s,w)=ϕT(s)w，我们有∇wv^(st,wt)=ϕ(s)\nabla_w \hat{v}(s_t, w_t)=\phi(s)∇w​v^(st​,wt​)=ϕ(s)将这个带入到TD算法wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \hat{v}(s_{t+1}, w_t)-\hat{v}(s_t,w_t)]\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​[rt+1​+γv^(st+1​,wt​)−v^(st​,wt​)]∇w​v^(st​,wt​)就变成了wt+1=wt+αt[rt+1+γϕT(st+1)wt−ϕT(st)wt]ϕ(st)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \phi^T(s_{t+1})w_t-\phi^T(s_t)w_t]\phi(s_t)wt+1​=wt​+αt​[rt+1​+γϕT(st+1​)wt​−ϕT(st​)wt​]ϕ(st​)这个具有线性函数近似的TD learning算法称为TD-Linear。
线性函数近似的劣势是：

• 难以去选择合适的feature vector.
  线性函数近似的优势是：
• TD算法在线性情况下的理论上的性质很容易理解和分析，与非线性情况相比
• 线性函数近似仍然在某些情况下使用：tabular representation是linear function approximation的一种少见的特殊情况。

那么为什么tabular representation是linear function approximation的一种少见的特殊情况？

• 首先，对于state sss，选择一个特殊的feature vectorϕ(s)=es∈R∣S∣\phi(s)=e_s\in \mathbb{R}^{|\mathcal{S}|}ϕ(s)=es​∈R∣S∣其中ese_ses​是一个vector，其中第sss个实体为1，其他为0.
• 在这种情况下v^(st,wt)=esTw=w(s)\hat{v}(s_t, w_t)=e_s^Tw=w(s)v^(st​,wt​)=esT​w=w(s)其中w(s)w(s)w(s)是www的第s个实体。

回顾TD-Linear算法：wt+1=wt+αt[rt+1+γϕT(st+1)wt−ϕT(st)wt]ϕ(st)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \phi^T(s_{t+1})w_t-\phi^T(s_t)w_t]\phi(s_t)wt+1​=wt​+αt​[rt+1​+γϕT(st+1​)wt​−ϕT(st​)wt​]ϕ(st​)

• 当ϕ(st)=es\phi(s_t)=e_sϕ(st​)=es​，上面的算法变成了wt+1=wt+αt[rt+1+γwt(st+1)−wt(st)]estw_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma w_t(s_{t+1})-w_t(s_t)]e_{s_t}wt+1​=wt​+αt​[rt+1​+γwt​(st+1​)−wt​(st​)]est​​这是一个向量等式，仅仅更新wtw_twt​的第sss个实体。
• 将上面式子两边乘以estTe_{s_t}^Test​T​，得到wt+1(st)=wt(st)+αt[rt+1+γwt(st+1)−wt(st)]w_{t+1}(s_t)=w_t(s_t)+\alpha_t[r_{t+1}+\gamma w_t(s_{t+1})-w_t(s_t)]wt+1​(st​)=wt​(st​)+αt​[rt+1​+γwt​(st+1​)−wt​(st​)]这就是基于表格形式的TD算法。

Illustrative examples

考虑一个5×5的网格世界示例：

• 给定一个策略：π(a∣s)=0.2\pi(a|s)=0.2π(a∣s)=0.2，对于任意的s,as,as,a
• 我们的目标是基于该策略，估计state values（策略评估问题）
• 总计有25种state values。
• 设置rforbidden=rboundary=−1,rtarget=1,γ=0.9r_{forbidden}=r_{boundary}=-1, r_{target}=1, \gamma=0.9rforbidden​=rboundary​=−1,rtarget​=1,γ=0.9
  

Ground truth:

• true state values和3D可视化
  

Experience samples：

• 500 episodes were generated following the given policy
• Each episode has 500 steps and starts from a randomly selected state-action pair following a uniform distribution。

为了对比，首先给出表格形式的TD算法（TD-Table）的结果：

那么看一下TD-Linear是否也能很好估计出来state value呢？
第一步就是要建立feature vector。要建立一个函数，这个函数也对应一个曲面，这个曲面能很好地拟合真实的state value对应的曲面。那么函数对应的曲面最简单的情况是什么呢？就是平面，所以这时候选择feature vector等于ϕ(s)=[1xy]∈R3\phi(s)=\begin{bmatrix}1 \\x \\y\end{bmatrix}\in \mathbb{R}^3ϕ(s)=​1xy​​∈R3在这种情况下，近似的state value是v^(s,w)=ϕT(s)w=[1,x,y][w1w2w3]=w1+w2x+w3y\hat{v}(s,w)=\phi^T(s)w=[1, x, y]\begin{bmatrix}w_1 \\w_2 \\w_3\end{bmatrix} =w_1+w_2x+w_3yv^(s,w)=ϕT(s)w=[1,x,y]​w1​w2​w3​​​=w1​+w2​x+w3​y注意，ϕ(s)\phi(s)ϕ(s)也可以定义为ϕ(s)=[x,y,1]T\phi(s)=[x, y, 1]^Tϕ(s)=[x,y,1]T，其中这里边的顺序是不重要的。

将刚才的feature vector带入TD-Linear算法中，得到:

• 这里边的趋势是正确的，但是有一些错误，这是由于用平面拟合的本身方法的局限性。
• 我们尝试使用一个平面去近似一个非平面，这是非常困难的。

为了提高近似能力，可以使用high-order feature vectors，这样也就有更多的参数。

• 例如，我们考虑这样一个feature vector：ϕ(s)=[1,x,y,x2,y2,xy]T∈R6\phi(s)=[1, x, y, x^2, y^2, xy]^T\in \mathbb{R}^6ϕ(s)=[1,x,y,x2,y2,xy]T∈R6在这种情况下，有v^(s,w)=ϕT(s)w=w1+w2x+w3y+w4x2+w5y2+w6xy\hat{v}(s,w)=\phi^T(s)w=w_1+w_2x+w_3y+w_4x^2+w_5y^2+w_6xyv^(s,w)=ϕT(s)w=w1​+w2​x+w3​y+w4​x2+w5​y2+w6​xy这对应一个quadratic surface。
• 可以进一步增加feature vector的维度ϕ(s)=[1,x,y,x2,y2,xy,x3,y3,x2y,xy2]T∈R10\phi(s)=[1, x, y, x^2, y^2, xy, x^3, y^3, x^2y, xy^2]^T\in \mathbb{R}^10ϕ(s)=[1,x,y,x2,y2,xy,x3,y3,x2y,xy2]T∈R10

通过higher-order feature vectors的TD-Linear算法的结果:

Summary of the story

1）首先从一个objective function出发J(w)=E[(vπ(S)−v^(S,w))2]J(w)=\mathbb{E}[(v_\pi(S)-\hat{v}(S, w))^2]J(w)=E[(vπ​(S)−v^(S,w))2]这个目标函数表明这是一个policy evaluation问题.
2）然后对这个objective function进行优化，优化方法使用gradient-descent algorithm:wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t (v_\pi(s_t)-\hat{v}(s_t,w_t))\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​(vπ​(st​)−v^(st​,wt​))∇w​v^(st​,wt​)但是问题是里边有一个vπ(st)v_\pi(s_t)vπ​(st​)是不知道的。
3）第三，使用一个近似替代算法中的true value function vπ(st)v_\pi(s_t)vπ​(st​)，得到下面算法：wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \hat{v}(s_{t+1}, w_t)-\hat{v}(s_t,w_t)]\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​[rt+1​+γv^(st+1​,wt​)−v^(st​,wt​)]∇w​v^(st​,wt​)

尽管上面的思路对于理解基本思想是非常有帮助的，但是它在数学上是不严谨的，因为做了替换操作。

Theoretical analysis

一个基本的结论，这个算法wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \hat{v}(s_{t+1}, w_t)-\hat{v}(s_t,w_t)]\nabla_w \hat{v}(s_t, w_t)wt+1​=wt​+αt​[rt+1​+γv^(st+1​,wt​)−v^(st​,wt​)]∇w​v^(st​,wt​)不是去minimize下面的objective function：J(w)=E[(vπ(S)−v^(S,w))2]J(w)=\mathbb{E}[(v_\pi(S)-\hat{v}(S, w))^2]J(w)=E[(vπ​(S)−v^(S,w))2]

实际上，有多种objective functions：

• Objective function 1：True value errorJ(w)=E[(vπ(S)−v^(S,w))2]=∣∣v^(w)−vπ∣∣D2J(w)=\mathbb{E}[(v_\pi(S)-\hat{v}(S, w))^2]=||\hat{v}(w)-v_\pi||_D^2J(w)=E[(vπ​(S)−v^(S,w))2]=∣∣v^(w)−vπ​∣∣D2​
• Objective function 2：Bellman errorJBE(w)=∣∣v^(w)−(rπ+γPπv^(w))∣∣D2≐∣∣v^(w)−Tπ(v^(w))∣∣D2J_{BE}(w)=||\hat{v}(w)-(r_\pi+\gamma P_{\pi}\hat{v}(w))||_D^2\doteq ||\hat{v}(w)-T_\pi(\hat{v}(w))||_D^2JBE​(w)=∣∣v^(w)−(rπ​+γPπ​v^(w))∣∣D2​≐∣∣v^(w)−Tπ​(v^(w))∣∣D2​其中Tπ(x)≐rπ+γPπxT_\pi(x)\doteq r_\pi+\gamma P_\pi xTπ​(x)≐rπ​+γPπ​x
• Objective function 2：Projected Bellman errorJPBE(w)=∣∣v^(w)−MTπ(v^(w))∣∣D2J_{PBE}(w)=||\hat{v}(w)-MT_\pi(\hat{v}(w))||_D^2JPBE​(w)=∣∣v^(w)−MTπ​(v^(w))∣∣D2​其中MMM是一个projection matrix（投影矩阵）

简而言之，上面提到的TD-Linear算法在最小化projected Bellman error。

Sarsa with function appriximation

到目前为止，我们仅仅是考虑state value estimation的问题，也就是我们希望v^≈vπ\hat{v}\approx v_\piv^≈vπ​。为了搜索最优策略，我们需要估计action values。

The Sarsa algorithm with value function approximation是：

这个上一节介绍的TD算法是一样的，只不过将v^\hat{v}v^换成了q^\hat{q}q^​

为了寻找最优策略，我们将policy evaluation（上面算法做的事儿）和policy improvement结合。下面给出Sarsa with function approximation的伪代码：

举个例子：

• Sarsa with linear function approximation。
• rforbidden=rboundary=−10,rtarget=1,γ=0.9,α=0.001,ϵ=0.1r_{forbidden}=r_{boundary}=-10, r_{target}=1, \gamma=0.9, \alpha=0.001, \epsilon=0.1rforbidden​=rboundary​=−10,rtarget​=1,γ=0.9,α=0.001,ϵ=0.1
  

Q-learning with function approximation

类似地，tabular Q-learning也可以扩展到value function approximation的情况。

The q-value更新规则是：

这与上面的Sarsa算法相同，除了q^(st+1,at+1,wt)\hat{q}(s_{t+1}, a_{t+1}, w_t)q^​(st+1​,at+1​,wt​)被替换为max⁡a∈A(st+1)q^(st+1,a,wt)\max_{a\in \mathcal{A}(s_{t+1})}\hat{q}(s_{t+1}, a, w_t)maxa∈A(st+1​)​q^​(st+1​,a,wt​)。

Q-learning with function approximation伪代码（on-policy version）：

举个例子：

• Q-learning with linear function approximation
• rforbidden=rboundary=−10,rtarget=1,γ=0.9,α=0.001,ϵ=0.1r_{forbidden}=r_{boundary}=-10, r_{target}=1, \gamma=0.9, \alpha=0.001, \epsilon=0.1rforbidden​=rboundary​=−10,rtarget​=1,γ=0.9,α=0.001,ϵ=0.1
  

Deep Q-learning

Deep Q-learning算法又被称为deep Q-network (DQN)：

• 最早的一个和最成功的一个将深度神经网络算法引入到强化学习中
• 神经网络的角色是一个非线性函数approximator
• 与下面的算法不同，是由于训练一个网络的方式：
  
  Deep Q-learning旨在最小化目标函数/损失函数：
  
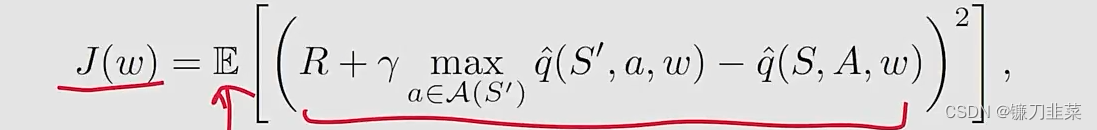
  其中(S,A,R,S′)(S,A,R,S')(S,A,R,S′)是随机变量。
  
  那么如何最小化目标函数呢？使用Gradient-descent！但是如何计算目标函数的梯度还是有一些tricky。这是因为在目标函数中有两个位置有www：
  
  也就是说参数w不仅仅只出现在q^(S,A,w)\hat{q}(S,A,w)q^​(S,A,w)中，还出现在它的前面。这里用yyy表示：y≐R+γmax⁡a∈A(S′)q^(S′,a,w)y\doteq R+\gamma \max_{a\in \mathcal{A}(S')} \hat{q}(S',a,w)y≐R+γa∈A(S′)max​q^​(S′,a,w)

为了简单起见，我们可以假设www在yyy中是固定的(至少一定时间内)，当我们计算梯度的时候。为了这样做，我们引入两个network。

• 一个是main network，用以表示q^(s,a,w)\hat{q}(s,a,w)q^​(s,a,w)
• 另一个是target network q^(s,a,wT)\hat{q}(s,a,w_T)q^​(s,a,wT​)

用这两个network吧上面目标函数中的两个q^\hat{q}q^​区分开来，就得到了如下式子：

其中wTw_TwT​是target network parameter。

当wTw_TwT​是固定的，可以计算出来JJJ的梯度如下：

• 这就是Deep Q-learning的基本思想，使用gradient-descent算法最小化目标函数。
• 然而，这样的优化过程涉及许多重要的技巧。

第一个技巧：使用了两个网络，一个是main network，另一个是target network。
为什么要使用两个网络呢？在数学上来说因为计算梯度的时候会非常的复杂，所以先去固定一个，然后再去计算另一个，这样就需要两个网络来实现。
具体实现的细节：

• 令www和wTw_TwT​分别表示mean network和target network的参数，它们初始化的时候是一样的。
• 在每个iteration中，从replay buffer中draw一个mini-batch样本{(s,a,r,s′)}\{(s,a,r,s')\}{(s,a,r,s′)}
• 网络的输入包括state sss和action aaa，目标输出是yT≐r+γmax⁡a∈A(s′)q^(s′,a,wT)y_T\doteq r+\gamma \max_{a\in \mathcal{A}(s')} \hat{q}(s',a,w_T)yT​≐r+γmaxa∈A(s′)​q^​(s′,a,wT​)。然后我们直接基于the mini-batch {(s,a,r,s′)}\{(s,a,r,s')\}{(s,a,r,s′)}最小化TD error或者称为loss function (yT−q^(s,a,w))2(y_T-\hat{q}(s,a,w))^2(yT​−q^​(s,a,w))2。这样一段时间后，参数w发生变化，再将其赋给wTw_TwT​，再用来训练www。

另一个技巧：Experience replay（经验回放）
问题：什么是Experience replay？
回答：

• 我们收集一些experience samples之后，we do NOT use these samples in the order they were collected。
• Instead，我们将它们存储在一个set中，称为replay buffer B≐{(s,a,r,s′)}\mathcal{B}\doteq \{(s, a, r, s')\}B≐{(s,a,r,s′)}
• 每次我们训练neural network，我们可以从replay buffer中draw a mini-batch的random samples
• 取出的samples，称为experience replay，应当按照一个均匀分布的方式，即每个experience被replay的机会是相等的。

问题：为什么在deep Q-learning中要用experience replay？为什么replay必须要按照一个uniform distribution的方式?
回答：这个回答依赖于下面的objective function

• (S,A)∼d(S,A)\sim d(S,A)∼d：(S,A)(S,A)(S,A)是一个索引，并将其视为一个single random variable。
• R∼p(R∣S,A),S′∼p(S′∣S,A)R\sim p(R|S,A), S'\sim p(S'|S,A)R∼p(R∣S,A),S′∼p(S′∣S,A)：RRR和SSS由system model确定
• state-action pair (S,A)(S,A)(S,A)的分布假定是uniform.
• 然而，样本采集不是按照均匀分布来的，因为它们是由某个policies按顺序生成的。
• 为了打破顺序采样样本的关联，我们才从replay buffer中按照uniformly方式drawing samples，也就是experience replay technique
• 这是在数学上为什么experience replay是必须的，以及为什么experience replay必须是uniform的原因。

回顾tabular的情况：

• 问题1：为什么tabular Q-learning没有要求experience replay？
  • 回答：没有uniform distribution的需要
• 问题2：为什么Deep Q-learning 涉及distribution？
  • 回答：因为在deep Q-learning的情况下，目标函数是一个在所有(S,A)(S,A)(S,A)之上的scale average。tabular case没有涉及SSS或者AAA的任何distribution。在tabular情况下算法旨在求解对于所有的(s,a)(s,a)(s,a)的一组方程（Bellman optimality equation）。
• 问题3：可以在tabular Q-learning中使用experience replay吗？
  • 回答：可以，而且还会让sample更加高效，因为同一个sample可以用多次。

再次给出Deep Q-learning的伪代码（off-policy version）：

需要澄清的几个问题：

• 为什么没有策略更新？因为这里是off-policy
• 为什么没有使用之前导出的梯度去更新策略？因为之前导出梯度的算法比较底层，它可以指导我们去生成现在的算法，但是要遵循神经网络批量训练的黑盒特性，然后更好地高效地训练神经网络
• 这里网络的input和output与DQN原文中的不一样。原文中是on-policy的，这里是off-policy的。

举个例子：目标是learn optimal action values for every state-action pair。一旦得到最优策略，最优greedy策略可以立即得到。
问题设置：

仿真结果：

如果我们仅仅使用100步的一个single episode将会发生什么？也就是数据不充分的情况

可以看出，好的算法是需要充分的数据才能体现效果的。

内容来源

1. 《强化学习的数学原理》 西湖大学工学院赵世钰教授 主讲
2. 《动手学强化学习》 俞勇 著