【AICG】2、扩散模型 | 到底什么是扩散模型?
文章目录
- 一、什么是扩散模型
- 二、扩散模型相关定义
- 2.1 符号和定义
- 2.2 问题规范化
- 三、可以提升的点
参考论文:A Survey on Generative Diffusion Model
github:https://github.com/chq1155/A-Survey-on-Generative-Diffusion-Model
一、什么是扩散模型
已经有大量的方法证明深度生成模型能够模拟人类的想象思维,生成人类难以分辨真伪的内容,主要方法如下:
- VAE:依赖于替代损失
- EBM
- GAN:因其对抗性训练性质而以潜在的不稳定训练和较少的生成多样性而闻名
- diffusion model

我们主要介绍扩散模型,扩散模型背后的直觉来源于物理学:
- 在物理学中,气体分子从高浓度区域扩散到低浓度区域
- 这与由于噪声的干扰而导致的信息丢失是相似的
- 通过引入噪声,然后尝试去噪来生成图像,模型每次在给定一些噪声输入的情况下学习生成新图像。
扩散模型可以用到哪些任务上:
- 计算机视觉
- 语言模型
- 声音模型
- AI for science
扩散模型的应用场景:
- 图文生成
- 视频生成
- 分子结构生成
- AI 绘画
- AI 制药
- …
扩散模型的工作原理:
- 学习由于噪声引起的信息衰减,然后使用学习到的模式来生成图像
扩散模型的结构:
- 扩散模型定义了一个扩散步骤的马尔可夫链,慢慢地向数据中添加随机噪声,然后学习反向扩散过程,从噪声中构建所需的数据样本
- 前向扩散过程:为输入图像 x0x_0x0 引入一系列的随机噪声,也就是对样本点分 T 步添加高斯噪声,随着噪声的引入,x0x_0x0 最终会失去区分特性,
- 反向恢复过程:从高斯先验出发,从有大量随机噪声的图中学习恢复原图
前向过程:

扩散模型相比 GAN 或 VAE 的缺点:
- 速度慢:扩散模型是基于马尔科夫过程来实现的,在训练和推理的时候都需要很多步骤

二、扩散模型相关定义
2.1 符号和定义
1、State:状态
State 是能够描述整个扩散模型过程的一系列数据:
- 初始状态:starting state x0x_0x0
- prior state:离散时为 xTx_TxT,连续时为 x1x_1x1
- 中间状态:intermediate state xtx_txt
2、Process 和 Transition Kernel
- Forward/Diffusion 过程 FFF:将初始状态转换到有噪声的状态
- Reverse/Denoised 过程 RRR:和前向过程方向相反,从有噪声的图像中逐步复原原图的过程
- Transition Kernel:在上面的两个过程中,每两个 state 的变换都是通过 transition kernel 来实现的,
前向和逆向的过程如下所示:

对于非离散情况,任何时间 0<=t 3、Pipeline: 假设定义 sampled data 为 x~0\widetilde{x}_0x0,则整个过程可以描述如下: 4、离散和连续过程 与离散过程相比,连续过程能够从任何时间状态中提取任何信息 如果扰动核的变化足够小,则连续过程有更好的理论支撑 5、训练目标 扩散模型是生成模型的一个子类,和 VAE 的目标函数类似,目标是让初始分布 x0x_0x0 和采样分布 x~0\widetilde{x}_0x0 尽可能的接近。 通过最大化如下 log-likelihood 公式来实现,其中 σ~\widetilde{\sigma}σ 在前向和逆向过程中是不同的: 1、Denoised Diffusion Probabilistic Model(DDPM):去噪扩散概率模型 NIPS 2021 的论文 ‘Denoising diffusion probabilistic models’ 中对扩散概率模型进行了改进,提出了 DDPM: DDPM Forward Process: DDPM 使用一系列的噪声系数 β1\beta_1β1、β2\beta_2β2 … βT\beta_TβT 作为不同时刻的 Markov trasition kernel。 一般都使用常数、线性规则、cosine 规则 来选择噪声系数,而且 [68] 中也证明了不同的噪声系数在实验中也没有明显的影响 DDPM 的前向过程定义如下: 根据从 x0x_0x0 到 xTx_TxT 的扩散步骤, Forward Diffusion Process 如下: DDPM Reverse Process: 逆向过程使用可学习的 Gaussian trasition 参数 θ\thetaθ 来定义如下: 逐步从 xTx_TxT 复原到 x0x_0x0 的过程如下,假设过程为 p(xT)=N(xT;0,I)p(x_T) = N(x_T;\ 0, I)p(xT)=N(xT; 0,I): 所以,pθ(x0)=∫pθ(x0:T)dx1:Tp_{\theta}(x_0)=\int p_{\theta}(x_{0:T})dx_{1:T}pθ(x0)=∫pθ(x0:T)dx1:T 的分布就是 x~0\widetilde{x}_0x0 的分布 Diffusion Training Objective:为了最小化 negative log-likelihood (NLL),则最小化问题转换为: 下图是 PPDM 的 pipeline: 2、Score Matching Formulation score matching 模型是为了解决原始数据分布的估计问题,通过近似数据的梯度 ∇xlogp(x)\nabla_xlogp(x)∇xlogp(x) 来实现,这也称为 score。 两个相邻状态的 transition kernel 为: Score matching 过程: score matching 的核心是训练一个得分估计网络 sθ(x,σ)s_{\theta}(x, \sigma)sθ(x,σ) 来预测得分。 DSM: 尽管扩散模型目前取得了很好的生成效果,到其逐步去噪的过程涉及非常多的迭代步骤,故此扩散模型的加速是很重要的研究课题。


2.2 问题规范化
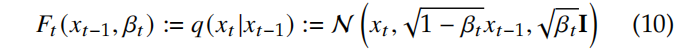

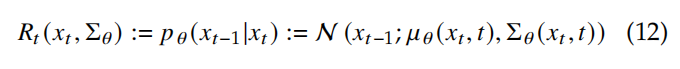







三、可以提升的点

