函数的连续性与间断点
创始人
2024-06-02 07:01:59
0次
连续性的概念及几何表达
我们用图像来对连续性进行表示：
函数连续性通俗的定义：当自变量x发生微小变化时，函数f(x)也发生微小变化，这就叫做函数的连续性。
函数连续的定义
当x趋近于x0时，f(x)接近于f(x0)
我们进行数学证明：
所以：
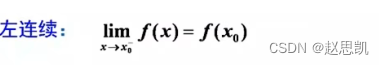
我们画出左连续的图像：
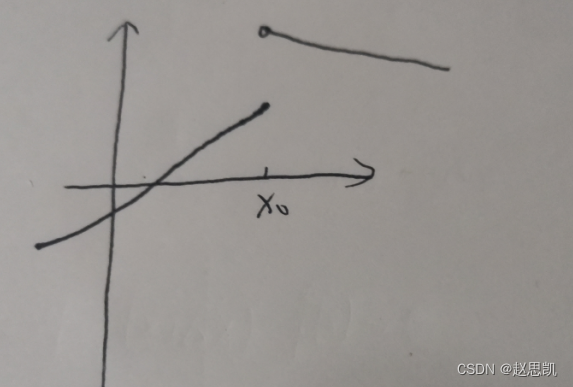
右连续和左连续类似，我们不再画图。
连续的充要条件是左连续并且右连续。
函数在区间连续的定义：
例如，f(x)在(a,b)上连续的定义：
f(x)在区间上的每一个点上都连续。
对于闭区间的连续，例如f(x)在[a,b]上连续的定义：
对于闭区间，我们要求左断点右连续，右端点左连续
函数连续的条件：
三个条件，第一个条件是有定义，第二个条件是极限存在，第三个条件是极限和函数值是相等的。
接下来，我们引入间断点：
间断点：
如果f(x)在x0的附近都没有定义，就不需要讨论函数是否连续或间断。
对于函数连续的判定条件中，只要这三条任意一条不满足就是间断。
函数间断点的分类
第一类间断点分为两种情况。
1：左右极限都存在并且相等。
我们可以修改这一点的函数值或者让这一点有定义来去掉这个间断点，所以这个间断点叫做可去间断点。
2：左右极限都存在但是不相等。
这就叫做跳跃间断点
第二类间断点
例题：
相关内容
热门资讯
繁华事散逐香尘
“繁华事散逐香尘”出处 出自 唐代 杜牧 的《金谷园》“繁华事散逐香尘”平仄韵脚 拼音：fán hu...
女子思念心上人的诗句
女子思念心上人的诗句 引导语：自古以来，亦流传下来了不少诗句，那么其中有哪些是写女子思念心上人的呢...
描与春天的花的诗句
描与春天的花的诗句 草色青青柳色黄， 桃花历乱李花香。 （贾至《春思》） 池塘生春草，园柳变鸣禽...
慨当初，倚飞何重，后来何酷
“慨当初，倚飞何重，后来何酷。”出处 出自 明代 文征明 的《满江红·拂拭残碑》“慨当初，倚飞何重，...
《王安石诗全集》(9)
《耿天骘惠梨次韵奉酬三首》 桐乡山远复川长，紫翠连城碧满隍。 今日桐乡谁爱我，当时我自爱桐乡...
莫言名言名句
莫言名言名句 导语：“思念一个人的滋味，就象是喝了一杯冰冷的水，然后一滴一滴凝成热泪。”下面是应届...
东指羲和能走马，海尘新生石山...
“东指羲和能走马，海尘新生石山下。”出处 出自 唐代 李贺 的《天上谣》“东指羲和能走马，海尘新生石...
寻胡隐君古诗-寻胡隐君 高启
寻胡隐君古诗-寻胡隐君 高启寻胡隐君古诗，是一首无言绝句诗，主要借景色叙述作者的好心情。本文由unj...
描写知己的抒情诗句
描写知己的抒情诗句 1、婴其呜矣，求其友声。——《诗经·小雅》 2、四海皆兄弟，谁为行路人。——...
现代爱国诗词
现代爱国诗词（精选8首） 热爱自己的祖国，爱国体现了人们对自己祖国的深厚感情，爱国是公民应有的道德...
谁问旗亭，美酒斗十千
“谁问旗亭，美酒斗十千。”出处 出自 宋代 贺铸 的《行路难·缚虎手》“谁问旗亭，美酒斗十千。”全诗...
寄托相思亲人的诗句
寄托相思亲人的诗句 别离是淡苦的水，孤独是一匙咖啡，我把相思煮得浓浓，品你留下的芳味。 寄托相思...
描写夏天傍晚的诗句
描写夏天傍晚的诗句 夏天的夜晚是什么样的?关于描写夏天夜晚的诗句有哪些?以下是小编为大家整理的'描...
桂花的诗句
关于桂花的诗句关于桂花的'诗句1 1、秦吟宿楚泽，海酒落桂花。 2 、去去陵阳东，行行芳桂丛。 ...
古诗草白居易一年级
古诗草白居易一年级 对于小草我们都不陌生了，以下是小编整理的古诗草白居易一年级，欢迎阅读参考！ ...
李贺的诗马诗
李贺的诗马诗 李贺的《马诗》共二十三首，这是第一首。这首诗开头一个“龙”字写此马非比寻常，又有背脊...
情谊的诗句
有关情谊的诗句（精选120句） 中国最早的诗句为律诗结构，格律要求严格，比如先秦时期的诗一般每句四...
菩萨蛮,菩萨蛮韩淲,菩萨蛮的...
菩萨蛮,菩萨蛮韩淲,菩萨蛮的意思,菩萨蛮赏析 -诗词大全 菩萨蛮,菩萨蛮韩淲,菩萨蛮的意思,菩萨蛮...
小升初语文文学知识点整理
小升初语文文学常识整理（苏教版） 1.儒家两大代表人物是：孔丘和孟子 2.文章西汉两司马：司...
写春草春花的诗句
写春草春花的诗句 春花秋草，只是催人老，总把千山眉黛扫。下文是有关写春草春花的诗句，欢迎大家阅读与...