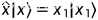Hermite矩阵的酉对角化
创始人
2024-06-03 07:01:41
0次
回顾有关定义
Hermite矩阵:一个矩阵将被称作Hermite矩阵,如果他的共轭转置等于他本身
对角化:对于矩阵M(n,n)若存在一个可逆矩阵A,使得A^(-1)MA为对角矩阵,则上一操作被称为矩阵的对角化
方阵可被对角化的条件:这个(n,n)矩阵存在n个线性不相关的特征向量
酉矩阵:一个矩阵将被称作酉矩阵如果其中列向量的模都为1且相互正交。实数域上的酉矩阵被称作正交矩阵
相似对角化
对于矩阵A,存在可逆矩阵P 使得
酉相似对角化:
对于矩阵A,存在正交矩阵Q 使得
量子力学基本定义
几率密度

量子力学名词解释
Hermitian operator
厄米算符是一种等于自己的厄米共轭的算符.量子力学中表示力学量的算符都是厄米算符
Uncertainty principle
设两厄米算符的对易关系为:

不确定关系:

Parity
将一个函数的所有坐标宗量改变符号的运算称为空间反演
Hermite 算符
实验上可观测的物理量的算符
现选取一个力学量完全集
 ,其Hermite算符记为
,其Hermite算符记为
任意态矢可以表示成

由各
 组成的列矢量就是
组成的列矢量就是 在表象中的波函数
在表象中的波函数
任何力学量算符
 在表象中的矩阵表示记为
在表象中的矩阵表示记为 ,其矩阵元
,其矩阵元
参考文献
米斌周 杨文光 Hermite 矩阵酉相似对角化的物理意义 华北科技学院学报 2011 年 10 月
上一篇:常见线程方法及线程状态
相关内容
热门资讯
少先队建队日主持词
少先队建队日主持词 什么是主持词 由主持人于节目进行过程中串联节目的串联词。如今的各种演出活动和...
晚会节目串词主持稿
晚会节目串词主持稿 在现在社会,很多地方都会使用到主持稿,通过主持稿的写作将主题贯穿于所有的节目之...
幼儿园开园揭牌剪彩仪式主持词
幼儿园开园揭牌剪彩仪式主持词 主持词要把握好吸引观众、导入主题、创设情境等环节以吸引观众。在一步步...
公司辞旧迎新晚会主持词串词
男:尊敬的各位领导、各位来宾, 女:亲爱的同事们 合:大家下午好! 男:光阴似箭,岁月如梭...
纯中式婚礼主持词
纯中式婚礼主持词(通用5篇) 主持词是主持人在台上表演的灵魂之所在。在现在的社会生活中,越来越多的...
悟空传的经典台词
悟空传的经典台词 1、我曾深爱过,我不在乎结局。 2、我知道天会愤怒,那,你知不知道,天也会颤抖...
最有创意的广告词(经典
最有创意的广告词(经典 01 钱不是问题,问题是没钱。 02 钻石恆久远,一颗就破產。 03 ...
毕业感谢致辞
关于毕业感谢致辞(精选15篇) 无论是在学校还是在社会中,大家都写过致辞吧,致辞的措词造句要考虑与...
年会嘉宾简短致辞
年会嘉宾简短致辞 在日复一日的学习、工作或生活中,大家总少不了要接触或使用致辞吧,致辞具有很强的实...
成长礼主持稿
成长礼主持稿(通用8篇) 在日常生活和工作中,需要使用主持稿的情况越来越多,主持稿是在晚会、联欢会...
电视剧《放羊的星星》经典台词
电视剧《放羊的星星》经典台词 在现实社会中,用到台词的地方越来越多,台词是一种特殊的,也是很难掌握...
抓周仪式主持词
抓周仪式主持词范文 主持词是主持人在台上表演的灵魂之所在。在如今这个中国,主持词是活动、集会等的必...
年终总结大会主持词结束语
年终总结大会主持词结束语 主持词是各种演出活动和集会中主持人串联节目的串联词。时代不断在进步,主持...
纯中式婚礼主持词(2)
让我们共同举起手中的酒杯,共同祝福我们这一对知心爱人,祝福他们在爱的旅途上风雨相承,相濡以沫,真爱一...
幼儿园园庆主持词
幼儿园园庆主持词 利用在中国拥有几千年文化的诗词能够有效提高主持词的感染力。在人们积极参与各种活动...
篮球比赛开幕式主持词
篮球比赛开幕式主持词(通用5篇) 主持词可以采用和历史文化有关的表述方法去写作以提升活动的文化内涵...
六一儿童节活动节目的主持词
六一儿童节活动节目的主持词(精选7篇) 主持词是各种演出活动和集会中主持人串联节目的串联词。在当今...
公司员工的感谢词
公司员工的感谢词3篇 我们虽然是公司的一名员工,其实也是公司的主人,需要有将公司当成家的态度,态度...
毕业晚会的主持稿
毕业晚会的主持稿(精选11篇) 在现在社会,我们很多时候都不得不用到主持稿,主持稿是主持人为节目进...
《加油金三顺》经典台词
《加油金三顺》经典台词 1、回忆是没有任何力量的。(三顺) 2、人都知道会死,但不还是活着吗?(...